
【题目】为了增强学生对新冠病毒预防知识的了解,我校初一年级开展了网上预防知识的宣传教育活动.为了解这次宣传教育活动的效果,学校从初一年级1500名学生中随机抽取部分学生进行网上知识测试(测试满分100分,得分均为整数),并根据抽取的学生测试成绩,制作了如下统计图表:
抽取学生知识测试成绩的频数表 | ||
成绩 | 频数(人) | 频率 |
| 10 | 0.1 |
| 15 |
|
|
| 0.2 |
| 40 |
|
|
|
|
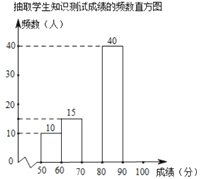
由图表中给出的信息回答下列问题:
(1)![]() ,
,![]() ,并补全频数直方图;
,并补全频数直方图;
(2)如果80分以上(包括80分)为优秀,请估计初一年级1500名学生中成绩优秀的人数;
(3)小强在这次测试中成绩为85分,你认为85分一定是这100名学生知识测试成绩的中位数吗?请简要说明理由.
【答案】(1)20,15,作图见解析;(2)825人;(3)不一定,理由见解析.
【解析】
(1)先求解出样本容量,用样本容量乘频率可求得m对应的频数;在用样本容量减去50至90分的频数得n对应的频数;
(2)先求出优秀的比例,再用比例乘总人数即可;
(3)排序后,仅能推断中位数在![]() 范围中,不能说明是85分
范围中,不能说明是85分
(1)样本容量为:10÷0.1=100人
则m=100×0.2=20
n=100-10-15-20-40=15;
补全频数直方图如下:
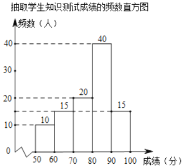
(2)![]() ,
,
答:全校1500名学生中成绩优秀的人数约为825人;
(3)不一定是,理由:将100名学生知识测试成绩从小到大排列,第50、51名的成绩都在分数段![]() 中,当他们的平均数不一定是85分.
中,当他们的平均数不一定是85分.


科目:初中数学 来源: 题型:
【题目】2018年5月13日,大国重器﹣﹣中国第一艘国产航母正式海试,某校团支部为了了解同学们对此事的知晓情况,随机抽取了部分同学进行调查,并根据收集到的信息绘制了如下两幅不完整的统计图,图中A表示“知道得很详细”,B表示“知道个大概”,C表示“听说了”,D表示“完全不知道”,请根据途中提供的信息完成下列问题:
(1)扇形统计图中A对应的圆心角是 度,并补全折线统计图.
(2)被抽取的同学中有4位同学都是班级的信息员,其中有一位信息员属于D类,校团支部从这4位信息员中随机选出两位作为校广播站某访谈节目的嘉宾,请用列表法或画树状图法,求出属于D类的信息员被选为的嘉宾的概率.
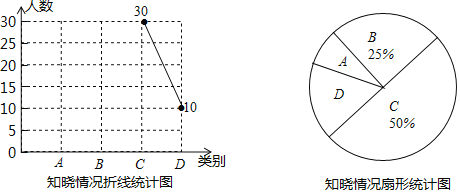
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
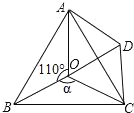
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在课外实践中,小明为了测量江中信号塔![]() 离河边的距离
离河边的距离![]() ,采取了如下措施:如图在江边
,采取了如下措施:如图在江边![]() 处,测得信号塔
处,测得信号塔![]() 的俯角为
的俯角为![]() ,若
,若![]() 米,
米,![]() ,
,![]() 米,
米,![]() 平行于
平行于![]() ,
,![]() 的坡度为
的坡度为![]() ,坡长
,坡长![]() 米,则
米,则![]() 的长为( )(精确到0.1米,参考数据:
的长为( )(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
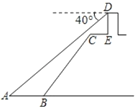
A.78.6米B.78.7米C.78.8米D.78.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出)
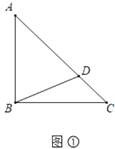
(1)如图①,在等腰![]() 中,斜边
中,斜边![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,则
,则![]() 的最小值为 .
的最小值为 .
(问题探究)
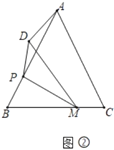
(2)如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,点
,点![]() 与点
与点![]() 对应,连接
对应,连接![]() ,求
,求![]() 的最小值.
的最小值.
(问题解决)
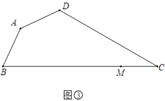
(3)如图③,四边形![]() 是规划中的休闲广场示意图,其中
是规划中的休闲广场示意图,其中![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() .现计划在四边形
.现计划在四边形![]() 内选取一点
内选取一点![]() ,把
,把![]() 建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路
建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路![]() 、
、![]() ,从实用和美观的角度,要求满足
,从实用和美观的角度,要求满足![]() ,且景观绿化区面积足够大,即
,且景观绿化区面积足够大,即![]() 区域面积尽可能小.则在四边形
区域面积尽可能小.则在四边形![]() 内是否存在这样的点
内是否存在这样的点![]() ?若存在,请求出
?若存在,请求出![]() 面积的最小值;若不存在,请说明理由.
面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y = ![]() ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
(1)求点D的坐标;
(2) ①若点C与点D关于x轴对称,且△BCD的面积等于4,求此二次函数的关系式;
②若CD=DB,且△BCD的面积等于4![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
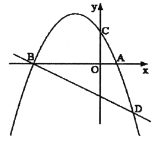
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,直线
点,直线![]() 交抛物线于点
交抛物线于点![]() ,并且,
,并且,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)已知点![]() 为抛物线上一动点,且在第二象限,顺次连接点
为抛物线上一动点,且在第二象限,顺次连接点![]() 、
、![]() 、
、![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
(3)在(2)中四边形![]() 面积最大的条件下,过点
面积最大的条件下,过点![]() 作直线平行于
作直线平行于![]() 轴,在这条直线上是否存在一个以
轴,在这条直线上是否存在一个以![]() 点为圆心,
点为圆心,![]() 为半径且与直线
为半径且与直线![]() 相切的圆?若存在,求出圆心
相切的圆?若存在,求出圆心![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=﹣x+2和抛物线![]() 相交于点A,B.
相交于点A,B.
(1)当k=![]() 时,求两函数图象的交点坐标;
时,求两函数图象的交点坐标;
(2)二次函数y2的顶点为P,PA或PB与直线y1=﹣x+2垂直时,求k的值.
(3)当﹣4<x<2时,y1>y2,试直接写出k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com