
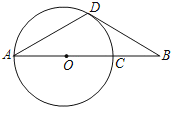
【题目】如图,线段AB经过⊙O的圆心O,交⊙O于A、C两点,BC=1,AD为⊙O的弦,连结BD,∠BAD=∠ABD=30°.
(1)求证:直线BD是⊙O的切线;
(2)求⊙O的半径长.
科目:初中数学 来源: 题型:
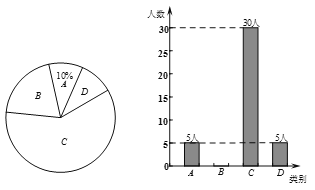
【题目】为了解阳光社区年龄20~60岁居民对垃圾分类的认识,学校课外实践小组随机抽取了该社区、该年龄段的部分居民进行了问卷调查,并将调查数据整理后绘成如下两幅不完整的统计图.图中A表示“全部能分类”,B表示“基本能分类”,C表示“略知一二”,D表示“完全不会”.请根据图中信息解答下列问题:
(1)补全条形统计图并填空:被调查的总人数是 人,扇形图中D部分所对应的圆心角的度数为 ;
(2)若该社区中年龄20~60岁的居民约3000人,请根据上述调查结果,估计该社区中C类有多少人?
(3)根据统计数据,结合生活实际,请你对社区垃圾分类工作提一条合理的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
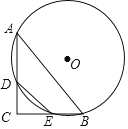
【题目】如图,在△ABC中,tan∠BACtan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△ABD中,∠DBA=∠CAB,AC与BD交于点F
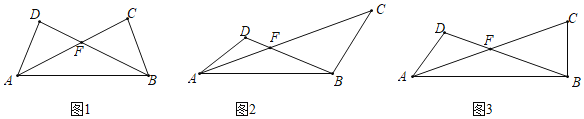
(1)如图1,若∠DAF=∠CBF,求证:AD=BC;
(2)如图2,∠D=135°,∠C=45°,AD=2,AC=4,求BD的长.
(3)如图3,若∠DBA=18°,∠D=108°,∠C=72°,AD=1,直接写出DB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
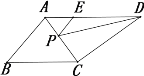
【题目】如图,四边形ABCD中,AD∥BC,AC平分∠BAD,∠ABC=60°,E为AD上一点,AE=2,DE=4,P为AC 上一点,则△PDE周长的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点A(-3,0),C(0,3),交x轴于另一点B,其顶点为D.
经过点A(-3,0),C(0,3),交x轴于另一点B,其顶点为D.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,直线CP交x轴于点E,若△CAE与△OCD相似,求P点坐标;
(3)如果点F在y轴上,点M在直线AC上,那么在抛物线上是否存在点N,使得以C,F,M,N为顶点的四边形是菱形?若存在,请求出菱形的周长;若不存在,请说明理由.
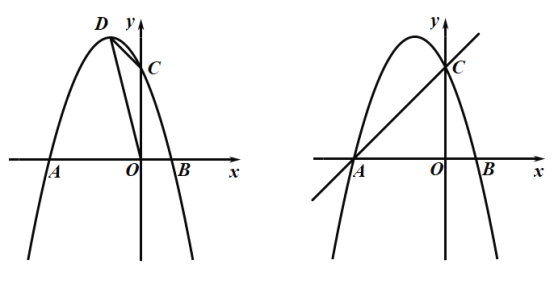
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△CDE中,∠ACB![]() ∠CDE
∠CDE![]() 90°,AC
90°,AC![]() BC,CD
BC,CD![]() ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
(1)如图1,当点D落在AC上时,DF与BE的数量关系是: ;
(2)如图2,当△CDE旋转到该位置时,DF与BE是否仍具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)如图3,当点E落在线段CB延长线上时,若CD![]() AC
AC![]() 2,求DF的长.
2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了缓解市区日益拥堵的交通状况,长沙市地铁建设工程指挥部对长沙地铁4号线茶子山站工程进行招标,接到了甲、乙两个工程队的指标书,从指标书中得知:甲工程队单独完成这项工程所需的时间是乙队单独完成这项工程所需的时间的3倍,若由甲队先做2个月,剩下的工程由甲、乙两队合作4个月可以完成.
(1)求甲、乙两队单独完成这项工程各需几个月?
(2)已知甲队每月的施工费用是76万元,乙队每月的施工费用是164万元,工程预算的施工费用为1000万元,为缩短工期以减少队交通的影响,拟安排甲、乙两队合作完成这项工程,则工程预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出拟的判断并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com