
ЁОЬтФПЁПЮЊСЫЛКНтЪаЧјШевцгЕЖТЕФНЛЭЈзДПіЃЌГЄЩГЪаЕиЬњНЈЩшЙЄГЬжИЛгВПЖдГЄЩГЕиЬњ4КХЯпВшзгЩНеОЙЄГЬНјааеаБъЃЌНгЕНСЫМзЁЂввСНИіЙЄГЬЖгЕФжИБъЪщЃЌДгжИБъЪщжаЕУжЊЃКМзЙЄГЬЖгЕЅЖРЭъГЩетЯюЙЄГЬЫљашЕФЪБМфЪЧввЖгЕЅЖРЭъГЩетЯюЙЄГЬЫљашЕФЪБМфЕФ3БЖЃЌШєгЩМзЖгЯШзі2ИідТЃЌЪЃЯТЕФЙЄГЬгЩМзЁЂввСНЖгКЯзї4ИідТПЩвдЭъГЩЃЎ
ЃЈ1ЃЉЧѓМзЁЂввСНЖгЕЅЖРЭъГЩетЯюЙЄГЬИїашМИИідТЃП
ЃЈ2ЃЉвбжЊМзЖгУПдТЕФЪЉЙЄЗбгУЪЧ76ЭђдЊЃЌввЖгУПдТЕФЪЉЙЄЗбгУЪЧ164ЭђдЊЃЌЙЄГЬдЄЫуЕФЪЉЙЄЗбгУЮЊ1000ЭђдЊЃЌЮЊЫѕЖЬЙЄЦквдМѕЩйЖгНЛЭЈЕФгАЯьЃЌФтАВХХМзЁЂввСНЖгКЯзїЭъГЩетЯюЙЄГЬЃЌдђЙЄГЬдЄЫуЕФЪЉЙЄЗбгУЪЧЗёЙЛгУЃПШєВЛЙЛгУЃЌашзЗМгдЄЫуЖрЩйЭђдЊЃПЧыИјГіФтЕФХаЖЯВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉввЖгЕЅЖРЭъГЩетЯюЙЄГЬаш6ИідТЃЌМзЖгЕЅЖРЭъГЩетЯюЙЄГЬаш18ИідТЃЛЃЈ2ЃЉЙЄГЬдЄЫуЕФЪЉЙЄЗбгУ1000ЭђдЊВЛЙЛгУЃЌашзЗМгдЄЫу80ЭђдЊЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЩшввЖгЕЅЖРЭъГЩетЯюЙЄГЬашxИідТЃЌМзЖгЕЅЖРЭъГЩетЯюЙЄГЬаш3xИідТЃЌгЩЬтвтПЩЕУЕШСПЙиЯЕЃКМзЕФЙЄзїаЇТЪЁС2+ЃЈМзЕФЙЄзїаЇТЪ+ввЕФЙЄзїаЇТЪЃЉЁС4=1ЃЌИљОнЕШСПЙиЯЕПЩЕУЗНГЬЃК![]() +(
+(![]() )
)![]() 4=1.НтЗНГЬПЩЕУД№АИЃЛ
4=1.НтЗНГЬПЩЕУД№АИЃЛ
ЃЈ2ЃЉЩшМзввСНИіЙЄГЬЖгКЯзїашвЊaИідТЭъГЩШЮЮёЃЌгЩЬтвтПЩЕУЕШСПЙиЯЕЃКЃЈМзЕФЙЄзїаЇТЪ+ввЕФЙЄзїаЇТЪЃЉЁСЙЄзїЪБМф=змЙЄзїСП1ЃЌИљОнЕШСПЙиЯЕСаЗНГЬЃЌЫуГіСНЖгКЯИЩашвЊЕФЪБМфЃЌдйИљОнЪБМфМЦЫуГіЗбгУМДПЩПДГі1000ЭђдЊЪЧЗёЙЛгУЃЎ
НтЃКЃЈ1ЃЉЩшввЖгЕЅЖРЭъГЩетЯюЙЄГЬаш![]() ИідТЃЌМзЖгЕЅЖРЭъГЩетЯюЙЄГЬаш
ИідТЃЌМзЖгЕЅЖРЭъГЩетЯюЙЄГЬаш![]() дТЃЌгЩЬтвтЕУЃК
дТЃЌгЩЬтвтЕУЃК
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ОМьбщЃК![]() ЪЧдЗНГЬЕФНтЃЌ
ЪЧдЗНГЬЕФНтЃЌ
дђМзЖгЕЅЖРЭъГЩетЯюЙЄГЬашвЊ![]() ИідТЃЌ
ИідТЃЌ
Д№ЃКввЖгЕЅЖРЭъГЩетЯюЙЄГЬаш6ИідТЃЌМзЖгЕЅЖРЭъГЩетЯюЙЄГЬаш18ИідТЃЎ
ЃЈ2ЃЉЩшМзЁЂввСНИіЙЄГЬЖгКЯзїашвЊ![]() ИідТЭъГЩШЮЮёЃЌгЩЬтвтЕУЃК
ИідТЭъГЩШЮЮёЃЌгЩЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌЪЉЙЄЗбгУЮЊЃК
ЃЌЪЉЙЄЗбгУЮЊЃК![]() ЃЈЭђдЊЃЉЃЌ
ЃЈЭђдЊЃЉЃЌ
Ёп![]() ЃЌЁрВЛЙЛгУЃЌ
ЃЌЁрВЛЙЛгУЃЌ
ашзЗМгЃК![]() ЃЈЭђдЊЃЉЃЌ
ЃЈЭђдЊЃЉЃЌ
Д№ЃКЙЄГЬдЄЫуЕФЪЉЙЄЗбгУ1000ЭђдЊВЛЙЛгУЃЌашзЗМгдЄЫу80ЭђдЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
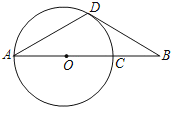
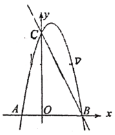
ЁОЬтФПЁПШчЭМЃЌЯпЖЮABОЙ§ЁбOЕФдВаФOЃЌНЛЁбOгкAЁЂCСНЕуЃЌBCЃН1ЃЌADЮЊЁбOЕФЯвЃЌСЌНсBDЃЌЁЯBADЃНЁЯABDЃН30ЁуЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпBDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓЁбOЕФАыОЖГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() жсе§АыжсЩЯвЛЖЏЕуЃЌдђ
жсе§АыжсЩЯвЛЖЏЕуЃЌдђ![]() ЖШЪ§ЮЊ_________ЃЌдкЕу
ЖШЪ§ЮЊ_________ЃЌдкЕу![]() дЫЖЏЕФЙ§ГЬжа
дЫЖЏЕФЙ§ГЬжа![]() ЕФзюаЁжЕЮЊ________ЃЎ
ЕФзюаЁжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
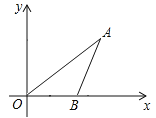
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНЉx2+2ЃЈmЉ2ЃЉx+3ЕФЭМЯѓгыxЁЂyжсНЛгкAЁЂBЁЂCШ§ЕуЃЌЦфжаAЃЈ3ЃЌ0ЃЉЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓmЕФжЕМАЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌШєЖЏЕуPдкЕквЛЯѓЯоФкЕФХзЮяЯпЩЯЃЌЖЏЕуNдкЖдГЦжс1ЩЯЃЌЕБPAЁЭNAЃЌЧвPAЃНNAЪБЃЌЧѓДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуQЪЧЖўДЮКЏЪ§ЭМЯѓЩЯЖдГЦжсгвВрвЛЕуЃЌЩшЕуQЕНжБЯпBCЕФОрРыЮЊdЃЌЕНХзЮяЯпЕФЖдГЦжсЕФОрРыЮЊd1ЃЌЕБ|dЉd1|ЃН2ЪБЃЌЧыЧѓГіЕуQЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгк
жсНЛгк![]() ЕуЃЌЕу
ЕуЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌКсзјБъЮЊ
ЩЯЃЌКсзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШЗЖЈЖўДЮКЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() НЛЖўДЮКЏЪ§
НЛЖўДЮКЏЪ§![]() ЕФЭМЯѓгкЕу
ЕФЭМЯѓгкЕу![]() ЕФУцЛ§МЧзї
ЕФУцЛ§МЧзї![]() ЮЊКЮжЕЪБ
ЮЊКЮжЕЪБ![]() ЕФжЕзюДѓЃЌВЂЧѓГі
ЕФжЕзюДѓЃЌВЂЧѓГі![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
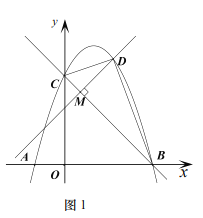
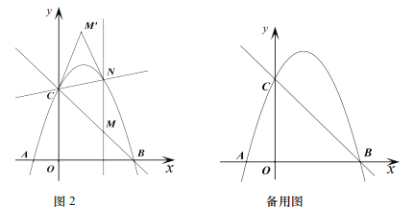
ЃЈ3ЃЉШчЭМ2ЃЌЙ§Еу![]() зї
зї![]() жсЕФЦНааЯпНЛЖўДЮКЏЪ§
жсЕФЦНааЯпНЛЖўДЮКЏЪ§![]() ЕФЭМЯѓгкЕу
ЕФЭМЯѓгкЕу![]() Еу
Еу![]() гыЕу
гыЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЖдГЦЪЧЗёДцдкЕу
ЖдГЦЪЧЗёДцдкЕу![]() ЪЙЫФБпаЮ
ЪЙЫФБпаЮ![]() ЮЊСтаЮЃЌШєДцдкжБНгаДГі
ЮЊСтаЮЃЌШєДцдкжБНгаДГі![]() ЕФжЕ;ШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ЕФжЕ;ШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓНЛxжсгкЕуAЃЌBЃЌНЛyжсгкЕуCЃЌвбжЊAЕФКсзјБъЮЊ
ЕФЭМЯѓНЛxжсгкЕуAЃЌBЃЌНЛyжсгкЕуCЃЌвбжЊAЕФКсзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓBЕуЕФКсзјБъКЭжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЖўДЮКЏЪ§ЕФЭМЯѓгавЛЕуDЃЌАбЕуDЯђзѓЦНвЦmЃЈ![]() ЃЉИіЕЅЮЛЃЌНЋгыИУЖўДЮКЏЪ§ЭМЯѓЩЯЕФСэвЛЕу
ЃЉИіЕЅЮЛЃЌНЋгыИУЖўДЮКЏЪ§ЭМЯѓЩЯЕФСэвЛЕу![]() жиКЯЃЌНЋ
жиКЯЃЌНЋ![]() ЯђЩЯвЦЖЏ5ИіЕЅЮЛКѓЃЌЧЁКУТфдкжБЯп
ЯђЩЯвЦЖЏ5ИіЕЅЮЛКѓЃЌЧЁКУТфдкжБЯп![]() ЩЯЃЌЧѓmЕФжЕЃЎ
ЩЯЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎЙћЩЬГЁОЯњвЛжжИпЕЕЫЎЙћЃЌдМлУПЧЇПЫ25дЊЃЌСЌајСНДЮеЧМлКѓУПЧЇПЫЫЎЙћЯждкЕФМлИёЮЊ36дЊЃЎ
ЃЈ1ЃЉШєУПДЮеЧМлЕФАйЗжТЪЯрЭЌЃЎЧѓУПДЮеЧМлЕФАйЗжТЪЃЛ
ЃЈ2ЃЉШєНјМлВЛБфЃЌАДЯжМлЪлГіЃЌУПЧЇПЫПЩЛёРћ15дЊЃЌЕЋИУЫЎЙћГіЯжжЭЯњЃЌЩЬГЁОіЖЈНЕМлmдЊГіЪлЃЌЭЌЪБАбНЕМлЕФЗљЖШmПижЦдк![]() ЕФЗЖЮЇЃЌОЪаГЁЕїВщЗЂЯжЃЌУПЬьЯњЪлСП
ЕФЗЖЮЇЃЌОЪаГЁЕїВщЗЂЯжЃЌУПЬьЯњЪлСП![]() ЃЈЧЇПЫЃЉгыНЕМлЕФЗљЖШmЃЈдЊЃЉГЩе§БШР§ЃЌЧвЕБ
ЃЈЧЇПЫЃЉгыНЕМлЕФЗљЖШmЃЈдЊЃЉГЩе§БШР§ЃЌЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ Чѓ
ЃЎ Чѓ![]() гы mЕФКЏЪ§НтЮіЪНЃЛ
гы mЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєЩЬГЁУПЬьЯњЪлИУЫЎЙћгЏРћ![]() дЊЃЌЮЊШЗБЃУПЬьгЏРћ
дЊЃЌЮЊШЗБЃУПЬьгЏРћ![]() зюДѓЃЌИУЫЎЙћУПЧЇПЫгІНЕМлЖрЩйдЊЃП
зюДѓЃЌИУЫЎЙћУПЧЇПЫгІНЕМлЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊгНг2022ФъЖЌАТЛсЃЌЙФРјИќЖрЕФДѓбЇЩњВЮгыЕНжОдИЗўЮёжаЃЌМзЁЂввСНЫљбЇаЃзщжЏСЫжОдИЗўЮёЭХЖгбЁАЮЛюЖЏЃЌОЙ§ГѕбЁЃЌСНЫљбЇаЃИїга300УћбЇЩњНјШызлКЯЫижЪеЙЪОЛЗНкЃЌЮЊСЫСЫНтетаЉбЇЩњЕФећЬхЧщПіЃЌДгСНаЃНјШызлКЯЫижЪеЙЪОЛЗНкЕФбЇЩњжаЗжБ№ЫцЛњГщШЁСЫ50УћбЇЩњЕФзлКЯЫижЪеЙЪОГЩМЈЃЈАйЗжжЦЃЉЃЌВЂЖдЪ§ОнЃЈГЩМЈЃЉНјааећРэЁЂУшЪіКЭЗжЮіЃЌЯТУцИјГіСЫВПЗжаХЯЂЃЎ
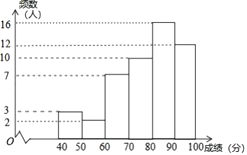
aЃЎМзбЇаЃбЇЩњГЩМЈЕФЦЕЪ§ЗжВМжБЗНЭМШчЭМЃЈЪ§ОнЗжГЩ6зщЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
bЃЎМзбЇаЃбЇЩњГЩМЈдк![]() етвЛзщЪЧЃК
етвЛзщЪЧЃК
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
cЃЎввбЇаЃбЇЩњГЩМЈЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ЁЂгХауТЪЃЈ85ЗжМАвдЩЯЮЊгХауЃЉШчЯТЃК
ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | гХауТЪ |
83.3 | 84 | 78 | 46% |
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉМзбЇаЃбЇЩњ![]() ЃЌввбЇаЃбЇЩњ
ЃЌввбЇаЃбЇЩњ![]() ЕФзлКЯЫижЪеЙЪОГЩМЈЭЌЮЊ82ЗжЃЌетСНШЫдкБОаЃбЇЩњжазлКЯЫижЪеЙЪОХХУћИќППЧАЕФЪЧ________ЃЈЬюЁА
ЕФзлКЯЫижЪеЙЪОГЩМЈЭЌЮЊ82ЗжЃЌетСНШЫдкБОаЃбЇЩњжазлКЯЫижЪеЙЪОХХУћИќППЧАЕФЪЧ________ЃЈЬюЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБЃЉЃЛ
ЁБЃЉЃЛ
ЃЈ2ЃЉИљОнЩЯЪіаХЯЂЃЌЭЦЖЯ________бЇаЃзлКЯЫижЪеЙЪОЕФЫЎЦНИќИпЃЌРэгЩЮЊЃК__________________________
ЃЈжСЩйДгСНИіВЛЭЌЕФНЧЖШЫЕУїЭЦЖЯЕФКЯРэадЃЉЃЎ
ЃЈ3ЃЉШєУПЫљбЇаЃзлКЯЫижЪеЙЪОЕФЧА120УћбЇЩњНЋБЛбЁШыжОдИЗўЮёЭХЖгЃЌдЄЙРМзбЇаЃЗжЪ§жСЩйДяЕН________ЗжЕФбЇЩњВХПЩвдШыбЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
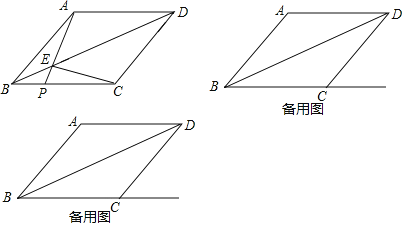
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDжаЃЌABЃН20ЃЌСЌНгBDЃЌЕуPЪЧЩфЯпBCЩЯвЛЕуЃЈВЛгыЕуBжиКЯЃЉЃЌAPгыЖдНЧЯпBDНЛгкЕуEЃЌСЌНгECЃЎ
ЃЈ1ЃЉЧѓжЄЃКAEЃНCEЃЛ
ЃЈ2ЃЉШєsinЁЯABDЃН![]() ЃЌЕБЕуPдкЯпЖЮBCЩЯЪБЃЌШєBPЃН8ЃЌЧѓЁїPECЕФУцЛ§ЃЛ
ЃЌЕБЕуPдкЯпЖЮBCЩЯЪБЃЌШєBPЃН8ЃЌЧѓЁїPECЕФУцЛ§ЃЛ
ЃЈ3ЃЉШєЁЯABCЃН45ЁуЃЌЕБЕуPдкЯпЖЮBCЕФбгГЄЯпЩЯЪБЃЌЧыЧѓГіЁїPECЪЧЕШбќШ§НЧаЮЪБBPЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com