
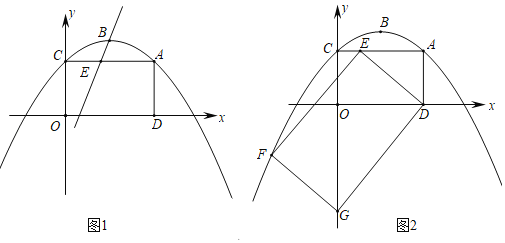
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 在直线
在直线![]() 上,横坐标为
上,横坐标为![]() .
.
(1)确定二次函数![]() 的解析式;
的解析式;
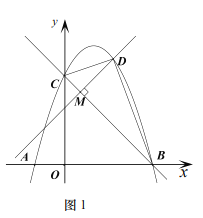
(2)如图1,![]() 时,
时,![]() 交二次函数
交二次函数![]() 的图象于点
的图象于点![]() 的面积记作
的面积记作![]() 为何值时
为何值时![]() 的值最大,并求出
的值最大,并求出![]() 的最大值;
的最大值;
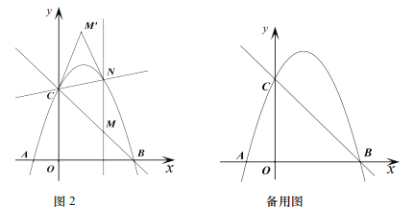
(3)如图2,过点![]() 作
作![]() 轴的平行线交二次函数
轴的平行线交二次函数![]() 的图象于点
的图象于点![]() 点
点![]() 与点
与点![]() 关于直线
关于直线![]() 对称是否存在点
对称是否存在点![]() 使四边形
使四边形![]() 为菱形,若存在直接写出
为菱形,若存在直接写出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
【答案】(1)![]() ;(2)m=
;(2)m=![]() ;
;![]() ;(3)存在,m的值为
;(3)存在,m的值为![]() 或
或![]() .
.
【解析】
(1)把点A、B的坐标代入![]() ,即可得到答案;
,即可得到答案;
(2)过点D作DE∥![]() 轴,交直线BC于点E,令点D(
轴,交直线BC于点E,令点D(![]() ,
,![]() ),则点E(
),则点E(![]() ,
,![]() ),易证
),易证![]() MED是等腰直角三角形,由
MED是等腰直角三角形,由![]() ,得到二次函数解析式,进而即可求解;
,得到二次函数解析式,进而即可求解;
(3)由题意得:当MN=MC时,四边形![]() 为菱形,设M(m,-m+3),则N(m,
为菱形,设M(m,-m+3),则N(m,![]() ),从而得MN,MC的表达式,列出关于m的方程,进而即可求解.
),从而得MN,MC的表达式,列出关于m的方程,进而即可求解.
(1)A(-1,0)、B(3,0)代入![]() 可得
可得![]() ,解得
,解得![]() ·
·
∴![]()
(2)过点D作DE∥![]() 轴,交直线BC于点E
轴,交直线BC于点E
∵![]()
∴点C(0,3)
∴直线BC:![]() ·
·
令点D(![]() ,
,![]() ),则点E(
),则点E(![]() ,
,![]() )
)
∴DE=![]()
∵OB=OC=3,
∴∠OBC=45°,
∵DE⊥x轴,
∴![]() MED是等腰直角三角形,
MED是等腰直角三角形,
∴MD=![]()
∴![]() ·
·
则![]() 时,
时,![]()
此时,点D(![]() ,
,![]() ),点E(
),点E(![]() ,
,![]() )
)
∴DE=![]() -
-![]() =
=![]() ,
,
∴m=![]() ;
;
(3)由题意得:当MN=MC时,四边形![]() 为菱形,
为菱形,
设M(m,-m+3),则N(m,![]() ),
),
∴MN=![]() ,MC=
,MC=![]() ,
,
∴![]() =
=![]() ,解得:m=
,解得:m=![]() 或
或![]()
![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ABC与△ABD中,∠DBA=∠CAB,AC与BD交于点F
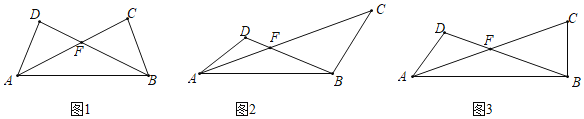
(1)如图1,若∠DAF=∠CBF,求证:AD=BC;
(2)如图2,∠D=135°,∠C=45°,AD=2,AC=4,求BD的长.
(3)如图3,若∠DBA=18°,∠D=108°,∠C=72°,AD=1,直接写出DB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2.
x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2.
(1)求抛物线的函数表达式和顶点B的坐标;
(2)如图1,抛物线与y轴交于点C,连接AC,过A作AD⊥x轴于点D,E是线段AC上的动点(点E不与A,C两点重合);
(i)若直线BE将四边形ACOD分成面积比为1:3的两部分,求点E的坐标;
(ii)如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在y轴上的同时点F恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
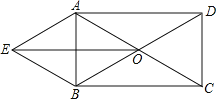
【题目】如图,矩形ABCD中,对角线AC,BD交于点O,以AD,OD为邻边作平行四边形ADOE,连接BE.
(1)求证:四边形AOBE是菱形;
(2)若∠EAO+∠DCO=180°,DC=3,求四边形ADOE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州中学在“读书日”期间购进一批图书, 需要用大小两种规格的纸箱来装运.![]() 个大纸箱和
个大纸箱和![]() 个小纸箱一次可以装
个小纸箱一次可以装![]() ,本书
,本书![]() 个大纸箱和
个大纸箱和![]() 个小纸箱--次可以装
个小纸箱--次可以装![]() 本书.
本书.
(1)一个大纸箱和一个小纸箱分别可以装多少本书?
(2)如果一共购入![]() 本书,每个纸箱恰好装满,分别需要用多少个大、小纸箱?
本书,每个纸箱恰好装满,分别需要用多少个大、小纸箱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了缓解市区日益拥堵的交通状况,长沙市地铁建设工程指挥部对长沙地铁4号线茶子山站工程进行招标,接到了甲、乙两个工程队的指标书,从指标书中得知:甲工程队单独完成这项工程所需的时间是乙队单独完成这项工程所需的时间的3倍,若由甲队先做2个月,剩下的工程由甲、乙两队合作4个月可以完成.
(1)求甲、乙两队单独完成这项工程各需几个月?
(2)已知甲队每月的施工费用是76万元,乙队每月的施工费用是164万元,工程预算的施工费用为1000万元,为缩短工期以减少队交通的影响,拟安排甲、乙两队合作完成这项工程,则工程预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出拟的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线![]() 与x轴,y轴分别交于点A,B,点
与x轴,y轴分别交于点A,B,点![]() 在第一象限内,连结
在第一象限内,连结![]() ,
,![]() ,
,![]() .动点P在
.动点P在![]() 上从点A向终点B匀速运动,同时,动点Q在
上从点A向终点B匀速运动,同时,动点Q在![]() 上从点C向终点O匀速运动,它们同时到达终点,连结
上从点C向终点O匀速运动,它们同时到达终点,连结![]() 交
交![]() 于点D.
于点D.
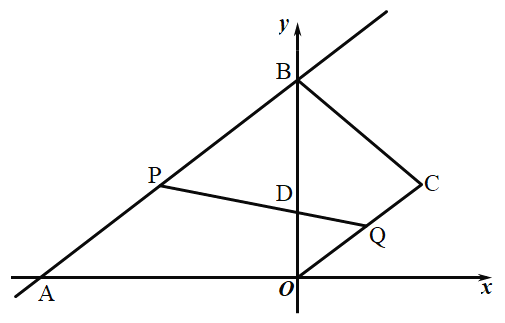
(1)求点B的坐标和a的值;
(2)当点Q运动到![]() 中点时,连结
中点时,连结![]() ,求
,求![]() 的面积;
的面积;
(3)作![]() 交直线
交直线![]() 于点R.
于点R.
①当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长度;
的长度;
②记![]() 交
交![]() 于点E,连结
于点E,连结![]() ,则
,则![]() 的最小值为__________.(直接写出答案)
的最小值为__________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=8,点P从点A出发,沿折线AC-CB以每秒2个单位长度的速度向终点B运动,当点P不与点A,B重合时,在边AB上取一点Q,满足∠PQA=2∠B,过点Q作QM⊥PQ,交边BC于点M,以PQ,QM为边作矩形PQMN,设点P的运动时间为t秒.

(1)直接写出线段PQ的长(用含t的代数式表示);
(2)当矩形PQMN为正方形时,求t的值;
(3)设矩形PQMN与△ABC重叠部分的面积为S,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于(﹣1,0),(3,0)两点,则下列判断中,错误的是( )

A.图象的对称轴是直线x=1
B.当﹣1<x<3时,y<0
C.当x>1时,y随x的增大而减小
D.一元二次方程中ax2+bx+c=0的两个根是﹣1和3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com