
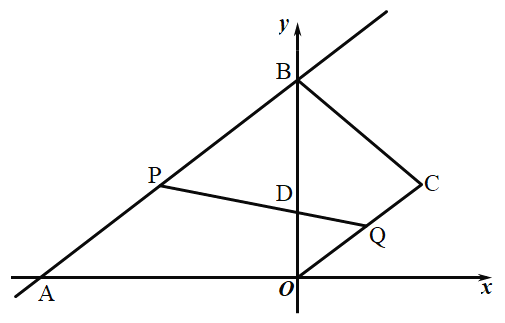
【题目】如图,在直角坐标系中,直线![]() 与x轴,y轴分别交于点A,B,点
与x轴,y轴分别交于点A,B,点![]() 在第一象限内,连结
在第一象限内,连结![]() ,
,![]() ,
,![]() .动点P在
.动点P在![]() 上从点A向终点B匀速运动,同时,动点Q在
上从点A向终点B匀速运动,同时,动点Q在![]() 上从点C向终点O匀速运动,它们同时到达终点,连结
上从点C向终点O匀速运动,它们同时到达终点,连结![]() 交
交![]() 于点D.
于点D.
(1)求点B的坐标和a的值;
(2)当点Q运动到![]() 中点时,连结
中点时,连结![]() ,求
,求![]() 的面积;
的面积;
(3)作![]() 交直线
交直线![]() 于点R.
于点R.
①当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长度;
的长度;
②记![]() 交
交![]() 于点E,连结
于点E,连结![]() ,则
,则![]() 的最小值为__________.(直接写出答案)
的最小值为__________.(直接写出答案)
【答案】(1)![]() ,
,![]() ;(2)6;(3)①
;(2)6;(3)①![]() 或
或![]() 或
或![]() ;②
;②![]()
【解析】
(1)根据![]() 令
令![]() 求算B的坐标;再根据
求算B的坐标;再根据![]() ,得出OC的斜率和AB的斜率相等进行求算;
,得出OC的斜率和AB的斜率相等进行求算;
(2)延长PQ与x轴交于G点,根据题意知:P点运动速度是Q点的两倍,得出点Q运动到![]() 中点时,P运动到AB中点,求出PQ的直线解析式从而得出G点的坐标,再根据
中点时,P运动到AB中点,求出PQ的直线解析式从而得出G点的坐标,再根据![]() 求算即可;
求算即可;
(3)①![]() ,设AP=2t,CQ=t,易得:
,设AP=2t,CQ=t,易得:![]()
![]() ,表示出P、Q、R的坐标,再根据
,表示出P、Q、R的坐标,再根据![]() 为等腰三角形分类讨论即可;
为等腰三角形分类讨论即可;
②根据①中P、Q的点坐标表示出PQ的函数解析式,从而求算D点坐标,再表示出E点坐标,根据距离公式表示出DE的长度,配方成顶点式求算最小值.
(1)∵直线![]() 与x轴,y轴分别交于点A,B
与x轴,y轴分别交于点A,B
∴![]()
又∵![]() ,点
,点![]()
∴![]() 即
即![]()
∴![]()
综上所述:B点坐标为![]() ,
,![]() ;
;
(2)延长PQ与x轴交于G点:
由(1)知:AB=10,OC=5, 根据题意知:P点运动速度是Q点的两倍
∴点Q运动到![]() 中点时,P运动到AB中点
中点时,P运动到AB中点
∴![]()
设PQ的解析式为:![]() ,代入得:
,代入得:
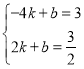 解得:
解得: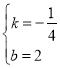
∴PQ的解析式为:![]()
∴![]()
∴![]()
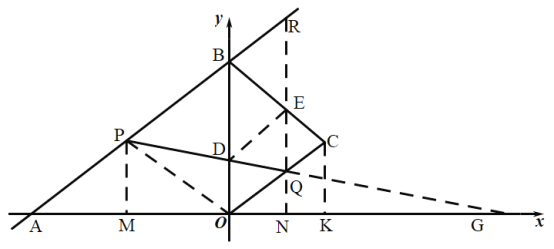
(3)①作![]()
根据题意知:P点运动速度是Q点的两倍,设AP=2t,CQ=t
易得:![]()
∴![]() ,代入得:
,代入得:
![]()
∴![]()
当![]() 时:根据三线合一知:
时:根据三线合一知:
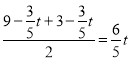 解得:
解得:![]()
∴CQ为![]() ;
;
当![]() 时:通过距离公式得:
时:通过距离公式得:
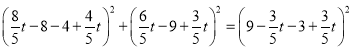 ,解得:
,解得:![]() (舍)
(舍)
∴CQ为![]() ;
;
当![]() 时,通过距离公式得:
时,通过距离公式得:
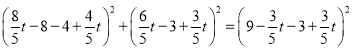 ,解得:
,解得:![]() (舍)
(舍)
∴CQ为![]()
综上所述:当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长
的长![]() 或
或![]() 或
或![]() ;
;
②设PQ的解析式为:![]() 代入P、Q:
代入P、Q:
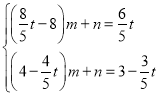 解得:
解得: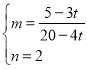
∴![]()
设BC的解析式为:![]() ,代入B、C得:
,代入B、C得:
![]() 解得
解得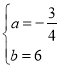
∴BC的解析式为:![]()
∴![]()
∴由距离公式得: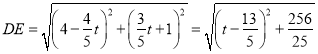
∴当![]() 时,DE有最小值为
时,DE有最小值为![]()
综上所述:DE最小值为![]()


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”,如10=3+7.
(1)从7,11,13,17这4个素数中随机抽取一个,则抽到的数是11的概率是_____;
(2)从7,11,13,17这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于24的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一座立交桥的示意图(道路宽度忽略不计),A为入口,F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF;弯道为以点O为圆心的一段弧,且所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥,均以8m/s的速度行驶,从不同出口驶出,其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示,结合题目信息,下列说法错误的是( )
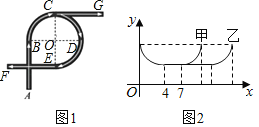
A.立交桥总长为168 m
B.从F口出比从G口出多行驶48m
C.甲车在立交桥上共行驶11 s
D.甲车从F口出,乙车从G口出
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 在直线
在直线![]() 上,横坐标为
上,横坐标为![]() .
.
(1)确定二次函数![]() 的解析式;
的解析式;
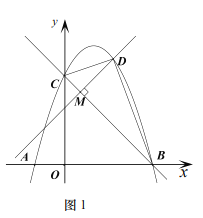
(2)如图1,![]() 时,
时,![]() 交二次函数
交二次函数![]() 的图象于点
的图象于点![]() 的面积记作
的面积记作![]() 为何值时
为何值时![]() 的值最大,并求出
的值最大,并求出![]() 的最大值;
的最大值;
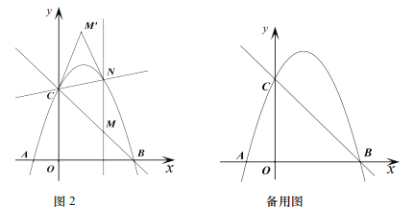
(3)如图2,过点![]() 作
作![]() 轴的平行线交二次函数
轴的平行线交二次函数![]() 的图象于点
的图象于点![]() 点
点![]() 与点
与点![]() 关于直线
关于直线![]() 对称是否存在点
对称是否存在点![]() 使四边形
使四边形![]() 为菱形,若存在直接写出
为菱形,若存在直接写出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
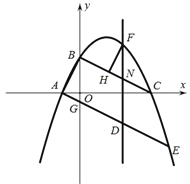
【题目】如图所示,在平面直角坐标系中,抛物线![]() 与y轴交于点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点
与y轴交于点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点![]() 为y轴负半轴上的一点,连接AG并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线交抛物线于点F,与线段BC交于点N.
为y轴负半轴上的一点,连接AG并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线交抛物线于点F,与线段BC交于点N.
(1)求抛物线的表达式及直线BC的表达式;
(2)在点D运动的过程中,当FN的值最大时,在线段BC上是否存在一点H,使得FNH与ABC相似,如果存在,求出此时H点的坐标;
(3)当DF=4时,连接DC,四边形ABCD先向上平移一定单位长度后,使点D落在x轴上,然后沿x轴向左平移n(1n4)个单位长度,用含n的表达式表示平移后的四边形与原四边形重叠部分的面积S(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商场经销一种高档水果,原价每千克25元,连续两次涨价后每千克水果现在的价格为36元.
(1)若每次涨价的百分率相同.求每次涨价的百分率;
(2)若进价不变,按现价售出,每千克可获利15元,但该水果出现滞销,商场决定降价m元出售,同时把降价的幅度m控制在![]() 的范围,经市场调查发现,每天销售量
的范围,经市场调查发现,每天销售量![]() (千克)与降价的幅度m(元)成正比例,且当
(千克)与降价的幅度m(元)成正比例,且当![]() 时,
时,![]() . 求
. 求![]() 与 m的函数解析式;
与 m的函数解析式;
(3)在(2)的条件下,若商场每天销售该水果盈利![]() 元,为确保每天盈利
元,为确保每天盈利![]() 最大,该水果每千克应降价多少元?
最大,该水果每千克应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“扶贫攻坚”活动中,某单位计划选购甲,乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.求甲,乙两种物品的单价各多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为3,A为圆内一定点,AO=1,P为圆上一动点,以AP为边作等腰△APQ,AP=PQ,∠APQ=120°,则OQ的最大值为( )
A.1+3![]() B.1+2
B.1+2![]() C.3+
C.3+![]() D.3
D.3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com