
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНЉ![]() x2+bx+cОЙ§ЕуAЃЈ4ЃЌ3ЃЉЃЌЖЅЕуЮЊBЃЌЖдГЦжсЪЧжБЯпxЃН2ЃЎ
x2+bx+cОЙ§ЕуAЃЈ4ЃЌ3ЃЉЃЌЖЅЕуЮЊBЃЌЖдГЦжсЪЧжБЯпxЃН2ЃЎ
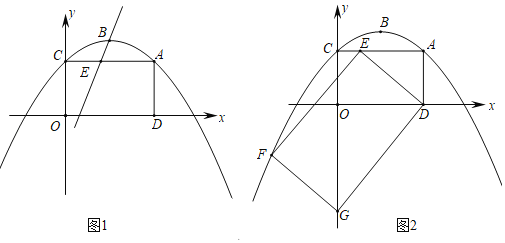
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНКЭЖЅЕуBЕФзјБъЃЛ
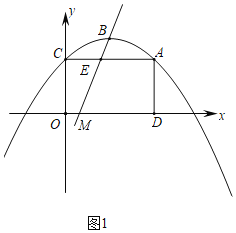
ЃЈ2ЃЉШчЭМ1ЃЌХзЮяЯпгыyжсНЛгкЕуCЃЌСЌНгACЃЌЙ§AзїADЁЭxжсгкЕуDЃЌEЪЧЯпЖЮACЩЯЕФЖЏЕуЃЈЕуEВЛгыAЃЌCСНЕужиКЯЃЉЃЛ
ЃЈiЃЉШєжБЯпBEНЋЫФБпаЮACODЗжГЩУцЛ§БШЮЊ1ЃК3ЕФСНВПЗжЃЌЧѓЕуEЕФзјБъЃЛ
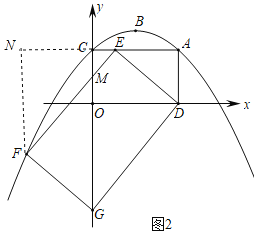
ЃЈiiЃЉШчЭМ2ЃЌСЌНгDEЃЌзїОиаЮDEFGЃЌдкЕуEЕФдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкЕуGТфдкyжсЩЯЕФЭЌЪБЕуFЧЁКУТфдкХзЮяЯпЩЯЃПШєДцдкЃЌЧѓГіДЫЪБAEЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() x2+x+3ЃЌЖЅЕуBЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЛЃЈ2ЃЉЃЈiЃЉЕуEЕФзјБъЮЊЃЈ
x2+x+3ЃЌЖЅЕуBЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЛЃЈ2ЃЉЃЈiЃЉЕуEЕФзјБъЮЊЃЈ![]() ЃЌ3ЃЉЛђЃЈ
ЃЌ3ЃЉЛђЃЈ![]() ЃЌ3ЃЉЃЛЃЈiiЃЉДцдкЃЛЕБЕуGТфдкyжсЩЯЕФЭЌЪБЕуFЧЁКУТфдкХзЮяЯпЩЯЃЌДЫЪБAEЕФГЄЮЊ
ЃЌ3ЃЉЃЛЃЈiiЃЉДцдкЃЛЕБЕуGТфдкyжсЩЯЕФЭЌЪБЕуFЧЁКУТфдкХзЮяЯпЩЯЃЌДЫЪБAEЕФГЄЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтЕУГі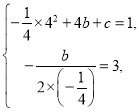 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌЕУГіХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃКyЃНЉ
ЃЌЕУГіХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃКyЃНЉ![]() x2+x+3ЃНЉ
x2+x+3ЃНЉ![]() ЃЈxЉ2ЃЉ2+4ЃЌМДПЩЕУГіЖЅЕуBЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЛ
ЃЈxЉ2ЃЉ2+4ЃЌМДПЩЕУГіЖЅЕуBЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЛ
ЃЈ2ЃЉЃЈiЃЉЧѓГіCЃЈ0ЃЌ3ЃЉЃЌЩшЕуEЕФзјБъЮЊЃЈmЃЌ3ЃЉЃЌЧѓГіжБЯпBEЕФКЏЪ§БэДяЪНЮЊЃКyЃН![]() x+
x+![]() ЃЌдђЕуMЕФзјБъЮЊЃЈ4mЉ6ЃЌ0ЃЉЃЌгЩЬтвтЕУГіOCЃН3ЃЌACЃН4ЃЌOMЃН4mЉ6ЃЌCEЃНmЃЌдђSОиаЮACODЃН12ЃЌSЬнаЮECOMЃН
ЃЌдђЕуMЕФзјБъЮЊЃЈ4mЉ6ЃЌ0ЃЉЃЌгЩЬтвтЕУГіOCЃН3ЃЌACЃН4ЃЌOMЃН4mЉ6ЃЌCEЃНmЃЌдђSОиаЮACODЃН12ЃЌSЬнаЮECOMЃН![]() ЃЌЗжСНжжЧщПіЧѓГіmЕФжЕМДПЩЃЛ
ЃЌЗжСНжжЧщПіЧѓГіmЕФжЕМДПЩЃЛ
ЃЈiiЃЉЙ§ЕуFзїFNЁЭACгкNЃЌдђNFЁЮCGЃЌЩшЕуFЕФзјБъЮЊЃКЃЈaЃЌЉ![]() a2+a+3ЃЉЃЌдђNFЃН3ЉЃЈЉ
a2+a+3ЃЉЃЌдђNFЃН3ЉЃЈЉ![]() a2+a+3ЃЉЃН
a2+a+3ЃЉЃН![]() a2ЉaЃЌNCЃНЉaЃЌжЄЁїEFNЁеЁїDGOЃЈASAЃЉЃЌЕУГіNEЃНODЃНACЃН4ЃЌдђAEЃНNCЃНЉaЃЌжЄЁїENFЁзЁїDAEЃЌЕУГі
a2ЉaЃЌNCЃНЉaЃЌжЄЁїEFNЁеЁїDGOЃЈASAЃЉЃЌЕУГіNEЃНODЃНACЃН4ЃЌдђAEЃНNCЃНЉaЃЌжЄЁїENFЁзЁїDAEЃЌЕУГі![]() ЃЌЧѓГіaЃНЉ
ЃЌЧѓГіaЃНЉ![]() Лђ0ЃЌЕБaЃН0ЪБЃЌЕуEгыЕуAжиКЯЃЌЩсШЅЃЌЕУГіAEЃНNCЃНЉaЃН
Лђ0ЃЌЕБaЃН0ЪБЃЌЕуEгыЕуAжиКЯЃЌЩсШЅЃЌЕУГіAEЃНNCЃНЉaЃН![]() ЃЌМДПЩЕУГіНсТлЃЎ
ЃЌМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЁпХзЮяЯпyЃНЉ![]() x2+bx+cОЙ§ЕуAЃЈ4ЃЌ3ЃЉЃЌЖдГЦжсЪЧжБЯпxЃН2ЃЌ
x2+bx+cОЙ§ЕуAЃЈ4ЃЌ3ЃЉЃЌЖдГЦжсЪЧжБЯпxЃН2ЃЌ
Ёр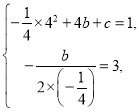
НтЕУ![]()
ЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃКyЃНЉ![]() x2+x+3ЃЌ
x2+x+3ЃЌ
ЁпyЃНЉ![]() x2+x+3ЃНЉ
x2+x+3ЃНЉ![]() ЃЈxЉ2ЃЉ2+4ЃЌ
ЃЈxЉ2ЃЉ2+4ЃЌ
ЁрЖЅЕуBЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЛ
ЃЈ2ЃЉЃЈiЃЉЁпyЃНЉ![]() x2+x+3ЃЌ
x2+x+3ЃЌ
ЁрxЃН0ЪБЃЌyЃН3ЃЌ
дђCЕуЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
ЁпAЃЈ4ЃЌ3ЃЉЃЌ
ЁрACЁЮODЃЌ
ЁпADЁЭxЃЌ
ЁрЫФБпаЮACODЪЧОиаЮЃЌ
ЩшЕуEЕФзјБъЮЊЃЈmЃЌ3ЃЉЃЌжБЯпBEЕФКЏЪ§БэДяЪНЮЊЃКyЃНkx+nЃЌжБЯпBEНЛxжсгкЕуMЃЌШчЭМ1ЫљЪОЃК
дђ![]()
НтЕУЃК  ЃЌ
ЃЌ
ЁржБЯпBEЕФКЏЪ§БэДяЪНЮЊЃКyЃН![]() x+
x+![]() ЃЌ
ЃЌ
СюЃКyЃН![]() x+
x+![]() ЃН0ЃЌдђxЃН4mЉ6ЃЌ
ЃН0ЃЌдђxЃН4mЉ6ЃЌ
ЁрЕуMЕФзјБъЮЊЃЈ4mЉ6ЃЌ0ЃЉЃЌ
ЁпжБЯпBEНЋЫФБпаЮACODЗжГЩУцЛ§БШЮЊ1ЃК3ЕФСНВПЗжЃЌ
ЁрЕуMдкЯпЖЮODЩЯЃЌЕуMВЛгыЕуOжиКЯЃЌ
ЁпCЃЈ0ЃЌ3ЃЉЃЌAЃЈ4ЃЌ3ЃЉЃЌMЃЈ4mЉ6ЃЌ0ЃЉЃЌEЃЈmЃЌ3ЃЉЃЌ
ЁрOCЃН3ЃЌACЃН4ЃЌOMЃН4mЉ6ЃЌCEЃНmЃЌ
ЁрSОиаЮACODЃНOCACЃН3ЁС4ЃН12ЃЌ
SЬнаЮECOMЃН![]() ЃЈOM+ECЃЉOCЃН
ЃЈOM+ECЃЉOCЃН![]() ЃЈ4mЉ6+mЃЉЁС3ЃН
ЃЈ4mЉ6+mЃЉЁС3ЃН![]() ЃЌ
ЃЌ
ЗжСНжжЧщПіЃК
Ђй![]() ЃН
ЃН![]() ЃЌМД
ЃЌМД ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУЃКmЃН![]() ЃЌ
ЃЌ
ЁрЕуEЕФзјБъЮЊЃКЃЈ![]() ЃЌ3ЃЉЃЛ
ЃЌ3ЃЉЃЛ
Ђк![]() ЃН
ЃН![]() ЃЌМД
ЃЌМД ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУЃКmЃН![]() ЃЌ
ЃЌ
ЁрЕуEЕФзјБъЮЊЃКЃЈ![]() ЃЌ3ЃЉЃЛ
ЃЌ3ЃЉЃЛ
злЩЯЫљЪіЃЌЕуEЕФзјБъЮЊЃКЃЈ![]() ЃЌ3ЃЉЛђЃЈ
ЃЌ3ЃЉЛђЃЈ![]() ЃЌ3ЃЉЃЛ
ЃЌ3ЃЉЃЛ
ЃЈiiЃЉДцдкЕуGТфдкyжсЩЯЕФЭЌЪБЕуFЧЁКУТфдкХзЮяЯпЩЯЃЛРэгЩШчЯТЃК
гЩЬтвтЕУЃКТњзуЬѕМўЕФОиаЮDEFGдкжБЯпACЕФЯТЗНЃЌ
Й§ЕуFзїFNЁЭACгкNЃЌдђNFЁЮCGЃЌШчЭМ2ЫљЪОЃК
ЩшЕуFЕФзјБъЮЊЃКЃЈaЃЌЉ![]() a2+a+3ЃЉЃЌ
a2+a+3ЃЉЃЌ
дђNFЃН3ЉЃЈЉ![]() a2+a+3ЃЉЃН
a2+a+3ЃЉЃН![]() a2ЉaЃЌNCЃНЉaЃЌ
a2ЉaЃЌNCЃНЉaЃЌ
ЁпЫФБпаЮDEFGгыЫФБпаЮACODЖМЪЧОиаЮЃЌ
ЁрЁЯDAEЃНЁЯDEFЃНЁЯNЃН90ЁуЃЌEFЃНDGЃЌEFЁЮDGЃЌACЁЮODЃЌ
ЁрЁЯNEFЃНЁЯODGЃЌЁЯEMCЃНЁЯDGOЃЌ
ЁпNFЁЮCGЃЌ
ЁрЁЯEMCЃНЁЯEFNЃЌ
ЁрЁЯEFNЃНЁЯDGOЃЌ
дкЁїEFNКЭЁїDGOжаЃЌЁЯNEF=ЁЯODGЃЌEF=DG,ЁЯEFN=ЁЯDGOЃЌ
ЁрЁїEFNЁеЁїDGOЃЈASAЃЉЃЌ
ЁрNEЃНODЃНACЃН4ЃЌ
ЁрACЉCEЃНNEЉCEЃЌМДAEЃНNCЃНЉaЃЌ
ЁпЁЯDAEЃНЁЯDEFЃНЁЯNЃН90ЁуЃЌ
ЁрЁЯNEF+ЁЯEFNЃН90ЁуЃЌЁЯNEF+ЁЯDEAЃН90ЁуЃЌ
ЁрЁЯEFNЃНЁЯDEAЃЌ
ЁрЁїENFЁзЁїDAEЃЌ/span>
Ёр![]() ЃЌМД
ЃЌМД![]() ЃН
ЃН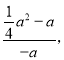
ећРэЕУЃК![]() a2+aЃН0ЃЌ
a2+aЃН0ЃЌ
НтЕУЃКaЃНЉ![]() Лђ0ЃЌ
Лђ0ЃЌ
ЕБaЃН0ЪБЃЌЕуEгыЕуAжиКЯЃЌ
ЁрaЃН0ЩсШЅЃЌ
ЁрAEЃНNCЃНЉaЃН![]() ЃЌ
ЃЌ
ЁрЕБЕуGТфдкyжсЩЯЕФЭЌЪБЕуFЧЁКУТфдкХзЮяЯпЩЯЃЌДЫЪБAEЕФГЄЮЊ![]() ЃЎ
ЃЎ


 КЎМйРждАББОЉНЬг§ГіАцЩчЯЕСаД№АИ
КЎМйРждАББОЉНЬг§ГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
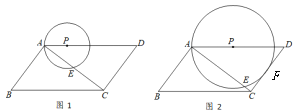
ЁОЬтФПЁПШчЭМ1ЃЌЦНааЫФБпаЮABCDжаЃЌABЁЭACЃЌABЃН3ЃЌADЃН5ЃЌЕуPдкБпADЩЯдЫЖЏЃЌвдPЮЊдВаФЃЌPAЮЊАыОЖЕФЁбPгыЖдНЧЯпACНЛгкAЃЌEСНЕуЃЎ
ЃЈ1ЃЉШчЭМ2ЃЌЕБЁбPгыБпCDЯрЧагкЕуFЪБЃЌЧѓAPЕФГЄЃЛ
ЃЈ2ЃЉВЛФбЗЂЯжЃЌЕБЁбPгыБпCDЯрЧаЪБЃЌЁбPгыЦНааЫФБпаЮABCDЕФБпгаШ§ИіЙЋЙВЕуЃЌЫцзХAPЕФБфЛЏЃЌЁбPгыЦНааЫФБпаЮABCDЕФБпЕФЙЋЙВЕуЕФИіЪ§вВдкБфЛЏЃЌШєЙЋЙВЕуЕФИіЪ§ЮЊ4ЃЌжБНгаДГіЯрЖдгІЕФAPЕФжЕЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжЛга1КЭЫќБОЩэСНИівђЪ§ЧвДѓгк1ЕФе§ећЪ§НазіЫиЪ§ЃЎЮвЙњЪ§бЇМвГТОАШѓИчЕТАЭКеВТЯыЕФбаОПжаШЁЕУСЫЪРНчСьЯШЕФГЩЙћЃЎИчЕТАЭКеВТЯыЪЧЁАУПИіДѓгк2ЕФХМЪ§ЖМБэЪОЮЊСНИіЫиЪ§ЕФКЭЁБЃЌШч10=3+7ЃЎ
ЃЈ1ЃЉДг7ЃЌ11ЃЌ13ЃЌ17ет4ИіЫиЪ§жаЫцЛњГщШЁвЛИіЃЌдђГщЕНЕФЪ§ЪЧ11ЕФИХТЪЪЧ_____ЃЛ
ЃЈ2ЃЉДг7ЃЌ11ЃЌ13ЃЌ17ет4ИіЫиЪ§жаЫцЛњГщШЁ1ИіЪ§ЃЌдйДггрЯТЕФ3ИіЪ§жаЫцЛњГщШЁ1ИіЪ§ЃЌгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓГщЕНЕФСНИіЫиЪ§жЎКЭЕШгк24ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
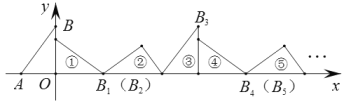
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуA(-1.5ЃЌ0)ЃЌB(0ЃЌ2)ЃЌНЋЁїABOЫГзХxжсЕФе§АыжсЮоЛЌЖЏЕФЙіЖЏЃЌЕквЛДЮЙіЖЏЕНЂйЕФЮЛжУЃЌЕуBЕФЖдгІЕуМЧзїB1ЃЛЕкЖўДЮЙіЖЏЕНЂкЕФЮЛжУЃЌЕуB1ЕФЖдгІЕуМЧзїB2ЃЛЕкШ§ДЮЙіЖЏЕНЂлЕФЮЛжУЃЌЕуB2ЕФЖдгІЕуМЧзїB3ЃЛ![]() ЃЛвРДЮНјааЯТШЅЃЌдђЕуB2020ЕФзјБъЮЊ__________ЃЎ
ЃЛвРДЮНјааЯТШЅЃЌдђЕуB2020ЕФзјБъЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
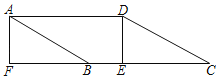
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЁЯCЃН30ЁуЃЌЙ§DзїDEЁЭBCгкЕуEЃЌбгГЄCBжСЕуFЃЌЪЙBFЃНCEЃЌСЌНгAFЃЎШєAFЃН4ЃЌCFЃН10![]() ЃЌдђABCDЕФУцЛ§ЮЊ_____ЃЎ
ЃЌдђABCDЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
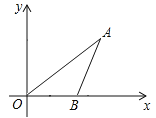
ЁОЬтФПЁПШчЭМЃЌвбжЊЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() жсе§АыжсЩЯвЛЖЏЕуЃЌдђ
жсе§АыжсЩЯвЛЖЏЕуЃЌдђ![]() ЖШЪ§ЮЊ_________ЃЌдкЕу
ЖШЪ§ЮЊ_________ЃЌдкЕу![]() дЫЖЏЕФЙ§ГЬжа
дЫЖЏЕФЙ§ГЬжа![]() ЕФзюаЁжЕЮЊ________ЃЎ
ЕФзюаЁжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЪЧвЛзљСЂНЛЧХЕФЪОвтЭМЃЈЕРТЗПэЖШКіТдВЛМЦЃЉЃЌAЮЊШыПкЃЌFЃЌGЮЊГіПкЃЌЦфжажБааЕРЮЊABЃЌCGЃЌEFЃЌЧвABЃНCGЃНEFЃЛЭфЕРЮЊвдЕуOЮЊдВаФЕФвЛЖЮЛЁЃЌЧвЫљЖдЕФдВаФНЧОљЮЊ90ЁуЃЎМзЁЂввСНГЕгЩAПкЭЌЪБЪЛШыСЂНЛЧХЃЌОљвд8m/sЕФЫйЖШааЪЛЃЌДгВЛЭЌГіПкЪЛГіЃЌЦфМфСНГЕЕНЕуOЕФОрРыyЃЈmЃЉгыЪБМфxЃЈsЃЉЕФЖдгІЙиЯЕШчЭМ2ЫљЪОЃЌНсКЯЬтФПаХЯЂЃЌЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
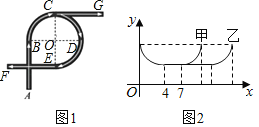
A.СЂНЛЧХзмГЄЮЊ168 m
B.ДгFПкГіБШДгGПкГіЖрааЪЛ48m
C.МзГЕдкСЂНЛЧХЩЯЙВааЪЛ11 s
D.МзГЕДгFПкГіЃЌввГЕДгGПкГі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгк
жсНЛгк![]() ЕуЃЌЕу
ЕуЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌКсзјБъЮЊ
ЩЯЃЌКсзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШЗЖЈЖўДЮКЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() НЛЖўДЮКЏЪ§
НЛЖўДЮКЏЪ§![]() ЕФЭМЯѓгкЕу
ЕФЭМЯѓгкЕу![]() ЕФУцЛ§МЧзї
ЕФУцЛ§МЧзї![]() ЮЊКЮжЕЪБ
ЮЊКЮжЕЪБ![]() ЕФжЕзюДѓЃЌВЂЧѓГі
ЕФжЕзюДѓЃЌВЂЧѓГі![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
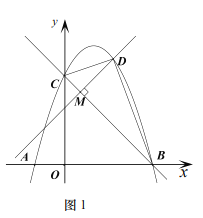
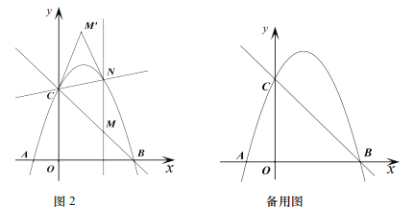
ЃЈ3ЃЉШчЭМ2ЃЌЙ§Еу![]() зї
зї![]() жсЕФЦНааЯпНЛЖўДЮКЏЪ§
жсЕФЦНааЯпНЛЖўДЮКЏЪ§![]() ЕФЭМЯѓгкЕу
ЕФЭМЯѓгкЕу![]() Еу
Еу![]() гыЕу
гыЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЖдГЦЪЧЗёДцдкЕу
ЖдГЦЪЧЗёДцдкЕу![]() ЪЙЫФБпаЮ
ЪЙЫФБпаЮ![]() ЮЊСтаЮЃЌШєДцдкжБНгаДГі
ЮЊСтаЮЃЌШєДцдкжБНгаДГі![]() ЕФжЕ;ШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ЕФжЕ;ШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЦНааЫФБпаЮABCDЕФЖдНЧЯпACЕФДЙжБЦНЗжЯпгыБпADЁЂBCЗжБ№ЯрНЛгкЕуEЁЂFЃЎ
ЧѓжЄЃКЫФБпаЮAFCEЪЧСтаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com