
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
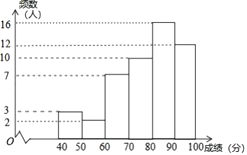
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.
【答案】(1)![]() ;(2)乙;理由见解析;(3)85.
;(2)乙;理由见解析;(3)85.
【解析】
(1)先算出甲校的中位数,发现A的成绩在中位数前,而读表得出B的成绩在中位线以下,以此判断排名;
(2)根据中位数和优秀率来判断综合素质;
(3)根据120人入选可算得入选比例,然后用比例乘抽样人数得出样本中入选人数,根据排名确定入选成绩即可.
(1)甲校共有50名学生,则中位数为第25位和第26位的平均成绩
由直方图和题干数据得,第25位和第26位的成绩为:81和81.5
∴中位数为:![]()
∵A成绩为82分,高于中位数,则A排名在甲校为前半部分
∵B成绩为82分,低于乙校中位数84,则B排名在乙校为后半部分
故A的排名更靠前;
(2)乙;
理由:①与甲校相比,乙校的中位数更高,说明乙校综合展示水平较高的同学更多;
②与甲校相比,乙校的优秀率更高,说明乙校综合展示水平高分的人数更多;
(3)∵120人入选,∴入选比例为:120÷300=40%
∵抽样50人,∴按照入选比例,抽样人数中,入选人数为:50×40%=20人
故选取前20名入选
根据直方图知,90-100段成绩有12人
故还需选取80-90段的前8名
由题干数据得,第8名为85分
故至少需要达到85分可入选


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴交于点B(6,0),与y轴交于点A,与二次函数y=ax2的图象在第一象限内交于点C(3,3).

(1)求此一次函数与二次函数的表达式;
(2)若点D在线段AC上,与y轴平行的直线DE与二次函数图象相交于点E,∠ADO=∠OED,求点D坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
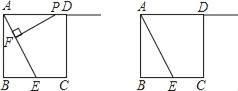
【题目】如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;
(3)试求当x取何值时,以D为圆心,DP为半径的⊙D与线段AE只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并用相关的思想方法解决问题.
例:若多项式![]() 分解因式的结果中有因式
分解因式的结果中有因式![]() ,求实数
,求实数![]() 的值.
的值.
解:设![]()
若![]() ,则
,则![]() 或
或![]()
由![]() 得
得![]()
则![]() 是方程
是方程![]() 的解
的解
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
解决问题:(1)若多项式![]() 分解因式的结果中有因式
分解因式的结果中有因式![]() ,求实数
,求实数![]() 的值;
的值;
(2)若多项式![]() 分解因式的结果中有因式
分解因式的结果中有因式![]() 和
和![]() .
.
①求出![]() 、
、![]() 的值;
的值;
②直接写出方程![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是抛物线的顶点,过点
是抛物线的顶点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
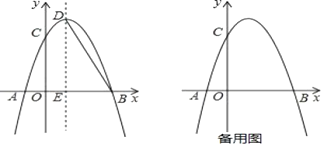
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上的动点,当
是抛物线上的动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)若点![]() 是
是![]() 轴上方抛物线上的动点,以
轴上方抛物线上的动点,以![]() 为边作正方形
为边作正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小、位置也随着改变,当顶点
的运动,正方形的大小、位置也随着改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,请直接写出点
轴上时,请直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() (a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;
(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.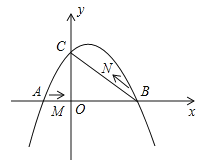
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,点P在对角线BD上(点P不与点B重合),连接AP,过点P作PE⊥AP交直线BC于点E.

(1)如图1,当AB=BC时,猜想线段PA和PE的数量关系: ;
(2)如图2,当AB≠BC时.求证:![]()
(3)若AB=8,BC=10,以AP,PE为边作矩形APEF,连接BF,当PE=![]() 时,直接写出线段BF的长.
时,直接写出线段BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com