
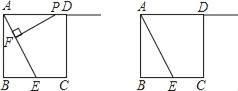
【题目】如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;
(3)试求当x取何值时,以D为圆心,DP为半径的⊙D与线段AE只有一个公共点.
【答案】(1)证明见解析;(2)满足条件的x的值为2或5;(3)当x=4-![]() 或x=4+
或x=4+![]() 或8<x≤4+2
或8<x≤4+2![]() 时,⊙D与线段AE只有一个公共点.
时,⊙D与线段AE只有一个公共点.
【解析】
(1)根据正方形的性质和PF⊥AE易证三角形相似.
(2)由于对应关系不确定,所以应针对不同的对应关系分情况考虑:当∠PEF=∠EAB时,则得到四边形ABEP为矩形,从而求得x的值;当∠PEF=∠AEB时,再结合△PFA∽△ABE,得到等腰△APE.再根据等腰三角形的三线合一得到F是AE的中点,运用勾股定理和相似三角形的性质进行求解.
(3)此题首先应针对点P的位置分为两种大情况:点P在AD边上时或当点P在AD的延长线上时.同时还要特别注意⊙D与线段AE只有一个公共点,不一定必须相切,只要保证和线段AE只有一个公共点即可.故求得相切时的情况和相交,但其中一个交点在线段AE外的情况即是x的取值范围.
(1)证明:∵正方形ABCD,
∴AD∥BC.
∴∠ABE=90°.
∴∠PAF=∠AEB.
又∵PF⊥AE,
∴∠PFA=∠ABE=90°.
∴△PFA∽△ABE.
(2)解:情况1,当△EFP∽△ABE,且∠PEF=∠EAB时,
则有PE∥AB
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
情况2,当△PFE∽△ABE,且∠PEF=∠AEB时,
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵![]() =
=![]() =
=![]() =
=![]() ,
,
∴EF=![]() AE=
AE=![]() .
.
∵![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴PE=5,即x=5.
∴满足条件的x的值为2或5.
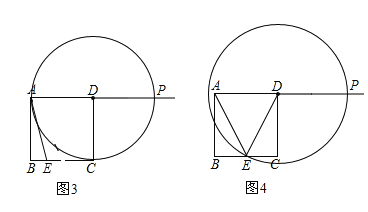
(3)解:如图,
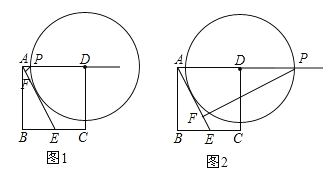
作DH⊥AE,则⊙D与线段AE的距离d即为DH的长,可得d=![]()
当点P在AD边上时,⊙D的半径r=DP=4﹣x;
当点P在AD的延长线上时,⊙D的半径r=DP=x﹣4;
如图1时,⊙D与线段AE相切,此时d=r,即![]() =4-x,∴x=4-
=4-x,∴x=4-![]() ;
;
如图2时,⊙D与线段AE相切,此时d=r,即![]() =x-4,∴x=4+
=x-4,∴x=4+![]() ;
;
如图3时,DA=PD,则PA=x=2DA=8
如图4时,当PD=ED时,
∵DE=![]() =2
=2![]() ,
,
∴PA=PD+AD=4+2![]() ,
,
∴当x=4-![]() 或x=4+
或x=4+![]() 或8<x≤4+2
或8<x≤4+2![]() 时,⊙D与线段AE只有一个公共点.
时,⊙D与线段AE只有一个公共点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
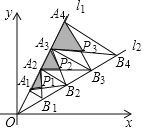
【题目】如图,A1,A2,A3…,An,An+1是直线![]() 上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线
上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线![]() 相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)
相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0,②4a﹣2b+c<0,③a﹣b+c=﹣9a,④若(﹣3,y1),(![]() ,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
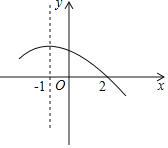
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1,3,则下列结论正确的个数有( )①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
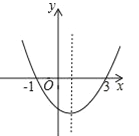
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )

A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点An______.
x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点An______.
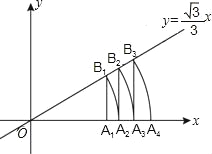
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
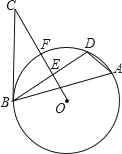
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
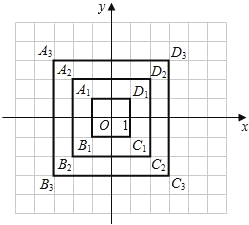
【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com