
【题目】如图,在平面直角坐标系中,抛物线![]() (a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;
(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.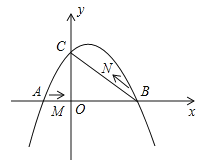
【答案】(1)![]() ;(2)S=
;(2)S=![]() ,运动1秒使△PBQ的面积最大,最大面积是
,运动1秒使△PBQ的面积最大,最大面积是![]() ;(3)t=
;(3)t=![]() 或t=
或t=![]() .
.
【解析】
(1)把点A、B、C的坐标分别代入抛物线解析式,列出关于系数a、b、c的解析式,通过解方程组求得它们的值;
(2)设运动时间为t秒.利用三角形的面积公式列出S△MBN与t的函数关系式.利用二次函数的图象性质进行解答;
(3)根据余弦函数,可得关于t的方程,解方程,可得答案.
(1)∵点B坐标为(4,0),抛物线的对称轴方程为x=1,
∴A(﹣2,0),把点A(﹣2,0)、B(4,0)、点C(0,3),
分别代入![]() (a≠0),得:
(a≠0),得:![]() ,解得:
,解得: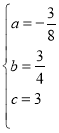 ,所以该抛物线的解析式为:
,所以该抛物线的解析式为:![]() ;
;
(2)设运动时间为t秒,则AM=3t,BN=t,∴MB=6﹣3t.
由题意得,点C的坐标为(0,3).在Rt△BOC中,BC=![]() =5.
=5.
如图1,过点N作NH⊥AB于点H,
∴NH∥CO,
∴△BHN∽△BOC,
∴![]() ,即
,即![]() ,
,
∴HN=![]() t,
t,
∴S△MBN=![]() MBHN=
MBHN=![]() (6﹣3t)
(6﹣3t)![]() t,
t,
即S=![]()
![]() ,
,
当△PBQ存在时,0<t<2,
∴当t=1时,S△PBQ最大=![]() .
.
答:运动1秒使△PBQ的面积最大,最大面积是![]() ;
;
(3)如图2,在Rt△OBC中,cos∠B=![]() .
.
设运动时间为t秒,则AM=3t,BN=t,∴MB=6﹣3t.
①当∠MNB=90°时,cos∠B=![]() ,即
,即![]() ,化简,得17t=24,解得t=
,化简,得17t=24,解得t=![]() ;
;
②当∠BMN=90°时,cos∠B=![]() ,化简,得19t=30,解得t=
,化简,得19t=30,解得t=![]() .
.
综上所述:t=![]() 或t=
或t=![]() 时,△MBN为直角三角形.
时,△MBN为直角三角形.
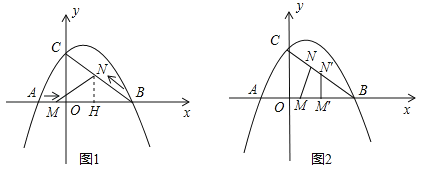


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】广宇、承义两名同学分别进行5次射击训练,训练成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
广宇 | 9 | 8 | 7 | 7 | 9 |
承义 | 6 | 8 | 10 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A.广宇训练成绩的平均数大于承义训练成绩平均数
B.广宇训练成绩的中位数与承义训练成绩中位数不同
C.广宇训练成绩的众数与承义训练成绩众数相同
D.广宇训练成绩比承义训练成绩更加稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知C是线段AB上的一点,分别以AC、BC为边在线段AB同侧作正方形ACDE和正方形CBGF,点F在CD上,联结AF、BD,BD与FG交于点M,点N是边AC上的一点,联结EN交AF 与点H.
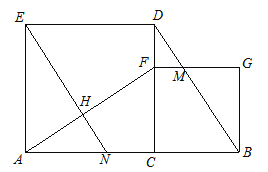
(1)求证:AF=BD;
(2)如果![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
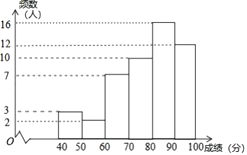
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现思考:已知等腰三角形ABC的两边分别是方程x2﹣7x+10=0的两个根,求等腰三角形ABC三条边的长各是多少?下边是涵涵同学的作业,老师说他的做法有错误,请你找出错误之处并说明错误原因.
涵涵的作业
解:x2﹣7x+10=0
a=1 b=﹣7 c=10
∵b2﹣4ac=9>0
∴x=![]() =
=![]()
∴x1=5,x2=2
所以,当腰为5,底为2时,等腰三角形的三条边为5,5,2.
当腰为2,底为5时,等腰三角形的三条边为2,2,5.
探究应用:请解答以下问题:
已知等腰三角形ABC的两边是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E是BC边的中点,动点M在CD边上运动,以EM为折痕将△CEM折叠得到△PEM,连接PA,若AB=4,∠BAD=60°,则PA的最小值是_____.
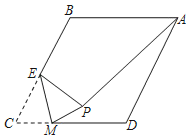
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,AB=4,以点B为圆心,BD长为半径的扇形EBF与AD,CD交于点G,H,且G,H分别为AD,CD边上的中点,则阴影部分的面积为____.
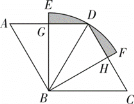
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平和中学以小元所在班级为例,对该班学生最喜爱参加的各类体育运动项目的情况进行了调査统计(最喜爱的项目只能选一项).并把调查的结果绘制成了如下图所示的两种不完全统计图,请你根据信息回答下列问题:

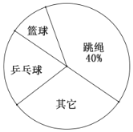
(1)小元所在的班级共有多少名学生?
(2)通过计算补全条形统计图
(3)如果平和中学总计有800名学生,请你估计全校学生中最喜欢参加篮球和最喜欢乒乓球运动共有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com