
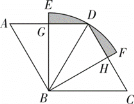
【题目】如图,在菱形ABCD中,∠BAD=60°,AB=4,以点B为圆心,BD长为半径的扇形EBF与AD,CD交于点G,H,且G,H分别为AD,CD边上的中点,则阴影部分的面积为____.
【答案】![]() -4
-4![]()
【解析】
在菱形ABCD中,∠BAD=60°,可得△ABD和△BDC是等边三角形,得AD=BD=AB=DC=4,根据G,H分别为AD,CD边上的中点,可得BG⊥AD,BH⊥DC,AG=DG=DH=CH=2,进而求得BG=BH=2![]() ,再根据阴影部分面积等于扇形EBF的面积减去两个三角形的面积即可求解.
,再根据阴影部分面积等于扇形EBF的面积减去两个三角形的面积即可求解.
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠BCD=∠BAD
又∵∠BAD=60°,
∴△ABD和△BDC是等边三角形,
∴AD=BD=AB=DC=4,
∵G,H分别为AD,CD边上的中点,
∴BG⊥AD,BH⊥DC,AG=DG=DH=CH=2,
∴∠DBG=∠DBH=30°,
∴BG=BH=2![]() ,
,
∴∠EBF=60°,
∴S阴影=S扇形EBF-S△BGD-S△BHD
=![]()
=![]() -4
-4![]() .
.
故答案为:![]() -4
-4![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
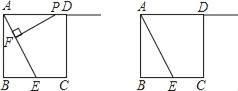
【题目】如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;
(3)试求当x取何值时,以D为圆心,DP为半径的⊙D与线段AE只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() (a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;
(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.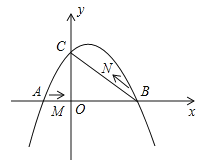
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 于
于![]() ,以
,以![]() 直径作
直径作![]() ,交
,交![]() 于点
于点![]() 恰有
恰有![]() ,连接
,连接![]() .
.
(1)如图1,求证:![]() ;
;
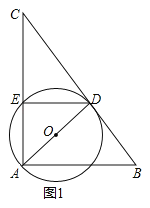
(2)如图2,连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() 连接
连接![]() 试探究
试探究![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;

(3)在(2)的基础上,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,且对角线AC⊥BD,垂足为点E,过点C作CF⊥AB于点F,交BD于点G.
(1)如图①,连接EF,若EF平分∠AFG,求证:AE=GE;
(2)如图②,连接CO并延长交AB于点H,若CH为∠ACF的平分线,AD=3,且tan∠FBG=![]() ,求线段AH长
,求线段AH长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们曾学过定理“在直角三角形中,如果一个锐角等于![]() ,那么它所对的直角边等于斜边的一半”,其逆命题也是成立的,即“在直角三角形中,如果一直角边等于斜边的一半,那么该直角边所对的角为
,那么它所对的直角边等于斜边的一半”,其逆命题也是成立的,即“在直角三角形中,如果一直角边等于斜边的一半,那么该直角边所对的角为![]() ”.如图,在
”.如图,在![]() 中,
中,![]() ,如果
,如果![]() ,那么
,那么![]() .
.
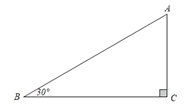
请你根据上述命题,解决下面的问题:

(1)如图1,![]() ,
,![]() 为格点,以
为格点,以![]() 为圆心,
为圆心,![]() 长为半径画弧交直线
长为半径画弧交直线![]() 于点
于点![]() ,则
,则![]() ______
______![]() ;
;
(2)如图2,![]() 、
、![]() 为格点,按要求在网格中作图(保留作图痕迹)。
为格点,按要求在网格中作图(保留作图痕迹)。
作![]() ,使点
,使点![]() 在直线
在直线![]() 上,并且
上,并且![]() ,
,![]() .
.
(3)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 内一点,
内一点,![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,点P在对角线BD上(点P不与点B重合),连接AP,过点P作PE⊥AP交直线BC于点E.

(1)如图1,当AB=BC时,猜想线段PA和PE的数量关系: ;
(2)如图2,当AB≠BC时.求证:![]()
(3)若AB=8,BC=10,以AP,PE为边作矩形APEF,连接BF,当PE=![]() 时,直接写出线段BF的长.
时,直接写出线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形AOBC的顶点B在y轴上,顶点A在反比例函数y=![]() 的图象上,边AC,OA分别交反比例函数y=
的图象上,边AC,OA分别交反比例函数y=![]() 的图象于点D,点E,边AC交x轴于点F,连接CE.已知四边形OBCE的面积为12,sin∠AOF=
的图象于点D,点E,边AC交x轴于点F,连接CE.已知四边形OBCE的面积为12,sin∠AOF=![]() ,则k的值为( )
,则k的值为( )
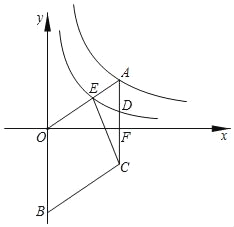
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com