
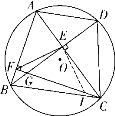
【题目】如图,四边形ABCD内接于⊙O,且对角线AC⊥BD,垂足为点E,过点C作CF⊥AB于点F,交BD于点G.
(1)如图①,连接EF,若EF平分∠AFG,求证:AE=GE;
(2)如图②,连接CO并延长交AB于点H,若CH为∠ACF的平分线,AD=3,且tan∠FBG=![]() ,求线段AH长
,求线段AH长

【答案】(1)见解析;(2)![]()
【解析】
(1)过点E作EF的垂线交CF于点I,证△EFI是等腰直角三角形,进而可证△AEF≌△GEI,等量代换即可证明结论;
(2)连接DO并延长,交⊙O于点P,连接AP,先求出圆的半径,再过点H作HJ⊥AC于点J,过点O作OK⊥AC于点K,根据三角函数可设设AJ=3t,则HJ=4t,由勾股定理可知AH=5t,根据角平分线的性质定理及三角函数用含有t的代数式表示出HF=HJ=4t,AF=9t,CF=CJ=12t,AC=15t,CK=![]() t,再根据平行线分线段成比例定理及勾股定理求解即可.
t,再根据平行线分线段成比例定理及勾股定理求解即可.
(1)如图,过点E作EF的垂线交CF于点I,
∵CF⊥AB,
∴∠AFG=90°,
∵EF平分∠AFG,
∴∠EFI=45°,
∵EF⊥EI,
∴∠EIF=45°,
∴EF=EI
又∵∠EGF+∠FAE=180°,∠EGF+∠EGI=180°,
∴∠EGI=∠FAE,
∵∠AEB=∠FEI=90°,
∴∠AEF=∠GEI,
∴△AEF≌△GEI(AAS),
∴AE=GE
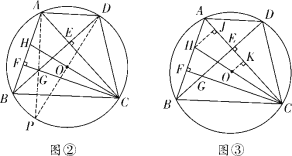
(2)如图②,连接DO并延长,交⊙O于点P,连接AP,
则∠ABD=∠P,
∵DP为⊙O的直径,
∴∠PAD=90°,
∵tan∠FBG=![]() ,
,
∴tanP=![]() =
=![]() ,
,
又∵AD=3,
∴AP=4,PD=5,
∴OD=![]()
∴OC=OD=![]()
如图③,过点H作HJ⊥AC于点J,过点O作OK⊥AC于点K,
∵HJ⊥AC,BD⊥AC,
∴HJ∥BD,
∴∠ABD=∠AHJ,则tan∠AHJ=![]() ,
,
设AJ=3t,则HJ=4t,由勾股定理可知AH=5t,
∵CH是∠ACF的平分线,且HF⊥CF,HJ⊥AC,
∴HF=HJ=4t,
∴AF=AH+HF=9t,
设CF=x,则CJ=x,
∵∠BFG=∠GEC,∠FGB=∠EGC,
∴∠FBG=∠ECG,
∴tan∠FCJ=![]() =
=![]() =
=![]() ,
,
解得x=12t,
∴CF=CJ=12t,
∴AC=15t,
∴CK=![]() t
t
又∵OK∥HJ,
∴![]() =
=![]() ,
,
∴OK=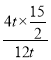 =
=![]() t,
t,
∴在Rt△OCK中,OK2+KC2=OC2,即(![]() t)2+(
t)2+(![]() t)2=(
t)2=(![]() )2,
)2,
解得t=![]() (负值舍去),
(负值舍去),
∴AH=5t=![]()


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
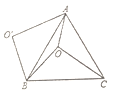
【题目】如图,O是等边![]() 内一点,
内一点,![]() ,以点B为旋转中心,将线段BO逆时针旋转
,以点B为旋转中心,将线段BO逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,则下列结论:
,则下列结论:
①![]() 可以由
可以由![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 得到
得到
②连接![]() ,则
,则![]()
③![]()
④![]()
其中正确的结论是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现思考:已知等腰三角形ABC的两边分别是方程x2﹣7x+10=0的两个根,求等腰三角形ABC三条边的长各是多少?下边是涵涵同学的作业,老师说他的做法有错误,请你找出错误之处并说明错误原因.
涵涵的作业
解:x2﹣7x+10=0
a=1 b=﹣7 c=10
∵b2﹣4ac=9>0
∴x=![]() =
=![]()
∴x1=5,x2=2
所以,当腰为5,底为2时,等腰三角形的三条边为5,5,2.
当腰为2,底为5时,等腰三角形的三条边为2,2,5.
探究应用:请解答以下问题:
已知等腰三角形ABC的两边是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是
是![]() 轴正半轴上的一动点,抛物线
轴正半轴上的一动点,抛物线![]() (
(![]() 是常数,且
是常数,且![]() 过点
过点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在点
在点![]() 左侧,连接
左侧,连接![]() ,以
,以![]() 为边做等边三角形
为边做等边三角形![]() ,点
,点![]() 与点
与点![]() 在直线
在直线![]() 两侧.
两侧.
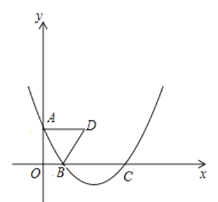
(1)求B、C的坐标;
(2)当![]() 轴时,求抛物线的函数表达式;
轴时,求抛物线的函数表达式;
(3)①求动点![]() 所成的图像的函数表达式;
所成的图像的函数表达式;
②连接![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,AB=4,以点B为圆心,BD长为半径的扇形EBF与AD,CD交于点G,H,且G,H分别为AD,CD边上的中点,则阴影部分的面积为____.
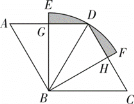
查看答案和解析>>
科目:初中数学 来源: 题型:
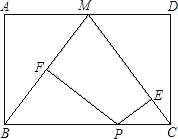
【题目】如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.
(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
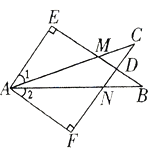
【题目】如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合“一带一路”国家倡议,某铁路货运集装箱物流园区正式启动了2期扩建工程一项地基基础加固处理工程由2、8两个工程公司承担建设,己知2工程公司单独建设完成此项工程需要180天![]() 工程公司单独施工天后,
工程公司单独施工天后,![]() 工程公司参与合作,两工程公司又共同施工
工程公司参与合作,两工程公司又共同施工![]() 天后完成了此项工程.
天后完成了此项工程.
(1)求![]() 工程公司单独建设完成此项工程需要多少天?
工程公司单独建设完成此项工程需要多少天?
(2)由于受工程建设工期的限制,物流园区管委会决定将此项工程划包成两部分,要求两工程公司同时开工,![]() 工程公司建设其中一部分用了
工程公司建设其中一部分用了![]() 天完成,
天完成,![]() 工程公司建设另一部分用了
工程公司建设另一部分用了![]() 天完成,其中
天完成,其中![]() ,
,![]() 均为正整数,且
均为正整数,且![]() ,
,![]() ,求
,求![]() 、
、![]() 两个工程公司各施工建设了多少天?
两个工程公司各施工建设了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
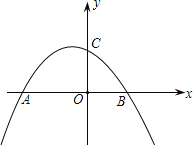
【题目】如图,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com