练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】平和中学以小元所在班级为例，对该班学生最喜爱参加的各类体育运动项目的情况进行了调査统计（最喜爱的项目只能选一项）．并把调查的结果绘制成了如下图所示的两种不完全统计图，请你根据信息回答下列问题：

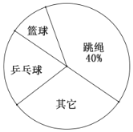
    （1）小元所在的班级共有多少名学生？

    （2）通过计算补全条形统计图

    （3）如果平和中学总计有800名学生，请你估计全校学生中最喜欢参加篮球和最喜欢乒乓球运动共有多少人．

    【答案】（1）50；（2）详见解析；（3）240

    【解析】

    （1）利用喜欢跳绳的人数除以其所占班级总人数的百分比即可求出结论；

    （2）利用班级总人数减去喜欢跳绳、乒乓球和其它的人数即可求出喜欢篮球的人数，然后补全条形统计图即可；

    （3）先求出最喜欢参加篮球和最喜欢乒乓球所占百分比再乘800即可．

    （1）（名）

    答：小元所在的班级共有50名学生

    （2）（名）

    ∴喜欢篮球运动的有5名学生

    补全图形如下

    （3）（人）

    答：全校学生中最喜欢篮球和乒乓球的共有240人

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B坐标为（4，0），抛物线的对称轴方程为x=1．

    （1）求抛物线的解析式；

    （2）点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN的面积为S，点M运动时间为t，试求S与t的函数关系，并求S的最大值；

    （3）在点M运动过程中，是否存在某一时刻t，使△MBN为直角三角形？若存在，求出t值；若不存在，请说明理由．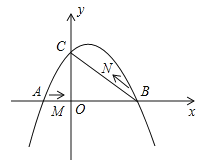

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们曾学过定理“在直角三角形中，如果一个锐角等于，那么它所对的直角边等于斜边的一半”，其逆命题也是成立的，即“在直角三角形中，如果一直角边等于斜边的一半，那么该直角边所对的角为”.如图，在中，，如果，那么.

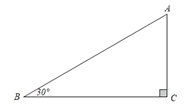
    请你根据上述命题，解决下面的问题：

    （1）如图1，，为格点，以为圆心，长为半径画弧交直线于点，则______；

    （2）如图2，、为格点，按要求在网格中作图（保留作图痕迹）。

    作，使点在直线上，并且，.

    （3）如图3，在中，，，为内一点，，于，且.

    ①求的度数；

    ②求证：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形ABCD中，点P在对角线BD上（点P不与点B重合），连接AP，过点P作PE⊥AP交直线BC于点E．

    （1）如图1，当AB＝BC时，猜想线段PA和PE的数量关系：　　；

    （2）如图2，当AB≠BC时．求证：

    （3）若AB＝8，BC＝10，以AP，PE为边作矩形APEF，连接BF，当PE＝时，直接写出线段BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形中，为线段上的动点（不含端点），将沿着翻折得到，

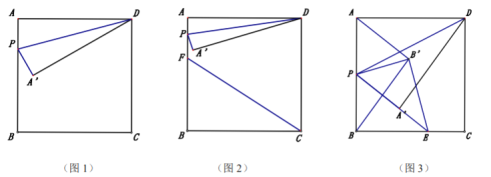
    （1）如图1，当，求长；

    （2）如图2，为线段上的点，当时，求点由到的运动过程中，线段扫过的图形与重叠部分的面积；

    （3）如图3，在上，连接，将沿着翻折得到，连结，问是否存在点，使得与相似？若存在，求出的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“自主互助学习型课堂竞赛”中，为奖励表现突出的同学，初一（7）班利用班费元钱，购买钢笔、相册、笔记本三种奖品，其中钢笔至多买支，若钢笔每支元，相册每本元，笔记本每本元，在把钱都用尽的条件下，买法共有（ ）

    A.种B.种C.种D.种

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，曲线是抛物线的一部分（其中是抛物线与轴的交点，是顶点），曲线是双曲线的一部分．曲线与组成图形．由点开始不断重复图形形成一组“波浪线”．若点，在该“波浪线”上，则的最大值为（ ）

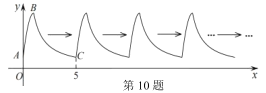
    A.5B.6C.2020D.2021

    查看答案和解析>>

    科目：初中数学 来源： 题型：

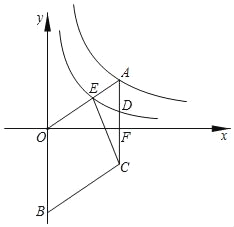
    【题目】如图所示，菱形AOBC的顶点B在y轴上，顶点A在反比例函数y＝的图象上，边AC，OA分别交反比例函数y＝的图象于点D，点E，边AC交x轴于点F，连接CE．已知四边形OBCE的面积为12，sin∠AOF＝ ，则k的值为（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题）用n个2×1矩形，镶嵌一个2×n矩形，有多少种不同的镶嵌方案？（2×n矩形表示矩形的邻边是2和n）

    （探究）不妨假设有an种不同的镶嵌方案．为探究an的变化规律，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进，最后猜想得出结论．

    探究一：用1个2×1矩形，镶嵌一个2×1矩形，有多少种不同的镶嵌方案？

    如图（1），显然只有1种镶嵌方案．所以，a1＝1．

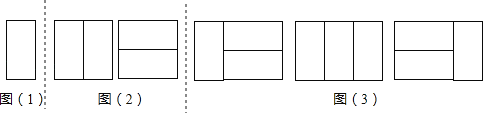
    探究二：用2个2×1矩形，镶嵌一个2×2矩形，有多少种不同的镶嵌方案？

    如图（2），显然只有2种镶嵌方案．所以，a2＝2．

    探究三：用3个2×1矩形，镶嵌一个2×3矩形，有多少种不同的镶嵌方案？

    一类：在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形，有1种镶嵌方案；

    二类：在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形，有2种镶嵌方案；

    如图（3）．所以，a3＝1+2＝3．

    探究四：用4个2×1矩形，镶嵌一个2×4矩形，有多少种不同的镶嵌方案？

    一类：在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形，有　 　种镶嵌方案；

    二类：在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形，有　 　种镶嵌方案；

    所以，a4＝　 　．

    探究五：用5个2×1矩形，镶嵌一个2×5矩形，有多少种不同的镶嵌方案？

    （仿照上述方法，写出探究过程，不用画图）

    ……

    （结论）用n个2×1矩形，镶嵌一个2×n矩形，有多少种不同的镶嵌方案？

    （直接写出an与an﹣1，an﹣2的关系式，不写解答过程）．

    （应用）用10个2×1矩形，镶嵌一个2×10矩形，有　 　种不同的镶嵌方案．

    查看答案和解析>>

    同步练习册答案