
【题目】某超市以20元/kg的价格购进一批商品进行销售,根据以往的销售经验及对市场行情的调研,该超市得到日销售量y(kg)与销售价格x(元/kg)之间的关系,部分数据如下表:
销售价格x(元/kg) | 25 | 30 | 35 | 40 | … |
日销售量y(kg) | 1000 | 800 | 600 | 400 | … |
(1)根据表中的数据,用所学过的函数知识确定y与x之间的函数关系式;
(2)超市应如何确定销售价格,才能使日销售利润W(元)最大?W最大值为多少?
(3)供货商为了促销,决定给予超市a元/kg的补贴,但希望超市在30≤x≤35时,最大利润不超过10240元,求a的最大值.
【答案】(1)![]() ;(2)销售价格为35元时,日销售利润W最大,最大利润为9000元;(3)a的最大值为2.
;(2)销售价格为35元时,日销售利润W最大,最大利润为9000元;(3)a的最大值为2.
【解析】
(1)首先根据表中的数据,可猜想y与x是一次函数关系,任选两点求表达式,再验证猜想的正确性;
(2)根据题意列出日销售利润w与销售价格x之间的函数关系式,根据二次函数的性质确定最大值即可;
(3)根据题意列出日销售利润w与销售价格x之间的函数关系式,并求得抛物线的对称轴,再分情况进行讨论,依据二次函数的性质求得a的值.
解:(1)观察表格,设y=kx+b,
得,![]() ,
,
解得![]() ,
,
∴![]() ,
,
检验:当x=25时,y=1000;当x=35时,y=600,符合上述函数式,
∴![]()
(2)由题得![]() =
=![]()
![]() ,
,
∵![]() <0,
<0,
∴当x=35时,W取最大值,最大值为9000元.
即销售价格为35元时,日销售利润W最大,最大利润为9000(元).
(3)由题得,![]() =
=![]()
![]() ,
,
对称轴![]() ,
,
若a≥10,则当x=30时,y有最大值,即W=800(10+a)>10240(舍去)
若0<a<10,则当![]() 时,y有最大值,即W=
时,y有最大值,即W=![]() ≤10240,
≤10240,
当![]() 时,
时,![]() 元,
元,
∴0<a≤2,
即a的最大值为2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,线段![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,
上一点,![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 的延长线上一点,且
的延长线上一点,且![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() 的半径为5,
的半径为5,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
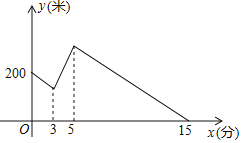
【题目】甲、乙两人分别从各自家出发乘坐出租车前往智博会,由于堵车,两人同时选择就近下车,已知甲车在乙车前面200米的A地下车,然后分别以各自的速度匀速走向会场,3分钟后,乙发现有物品遗落在出租车上,于是立即以不变的速度返回寻找,找到出租车时,出租车恰好向会场方向行驶了100米,乙拿到物品后立即以原速返回继续走向会场,同时甲以先前速度的一半走向会场,又经过10分钟,乙在B地追上甲,两人随后一起以甲放慢后的速度行走1分钟到达会场,甲、乙两人相距的路程y(m)与甲行走的时间x(min)之间的关系如图所示,(乙拿物品的时间忽略不计),则A地距离智博会会场的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是: ;
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于4的概率(请用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
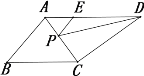
【题目】如图,四边形ABCD中,AD∥BC,AC平分∠BAD,∠ABC=60°,E为AD上一点,AE=2,DE=4,P为AC 上一点,则△PDE周长的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
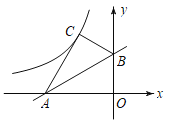
【题目】如图,已知直线![]() 与x轴,y轴分别交于点A,B,将△ABO沿直线AB翻折后得到△ABC,若反比例函数
与x轴,y轴分别交于点A,B,将△ABO沿直线AB翻折后得到△ABC,若反比例函数![]() (x<0)的图象经过点C,则k=______.
(x<0)的图象经过点C,则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
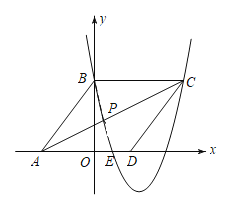
【题目】如图,在平面直角坐标系中,菱形ABCD的三个顶点A,B,D在坐标轴上,且已知点A(![]() ,
,![]() ),点B(
),点B(![]() ,
,![]() ),现有抛物线m经过点B,C和OD的中点.
),现有抛物线m经过点B,C和OD的中点.
(1)求抛物线m的解析式;
(2)在抛物线![]() 上是否存在点P,使得
上是否存在点P,使得![]() ?若存在,求出点P的坐标,若不存在,请说明理由;
?若存在,求出点P的坐标,若不存在,请说明理由;
(3)抛物线m与x轴的另一交点为F,M是线段AC上一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣![]() x+3的图象与反比例函数y=
x+3的图象与反比例函数y=![]() 的图象相交于A(m,6),B两点.
的图象相交于A(m,6),B两点.
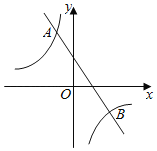
(1)求反比例函数的表达式及点B的坐标;
(2)点P在x轴上,连接AP,BP,若△ABP的面积为18,求满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为推荐选手参加学校举办的“祖国在我心中”演讲比赛活动,先在班级中进行预赛,班主任根据学生的成绩从高到低划分为A,B,C,D四个等级,并绘制了不完整的两种统计图表.请根据图中提供的信息,回答下列问题:
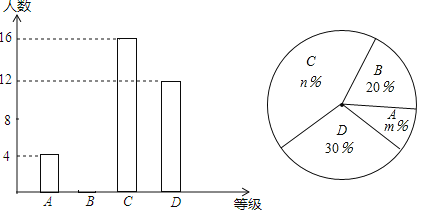
(1)a的值为 ;
(2)求C等级对应扇形的圆心角的度数;
(3)获得A等级的4名学生中恰好有1男3女,该班将从中随机选取2人,参加学校举办的演讲比赛,请利用列表法或画树状图法,求恰好选中一男一女参加比赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com