
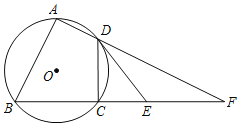
【题目】如图,四边形ABCD内接于⊙O,AB=AC,∠BAD=90°,延长AD,BC交于点F.过点D作⊙O的切线,交BF于点E.
(1)求证:DE=EF;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接BD,由AB=AC知∠ABC=∠ADB,证∠ABC=∠CDF得∠CDF=∠ADB.由∠BAD=90°知BD为⊙O的直径,据此得∠F+∠CDF=90°,结合DE为⊙O的切线得∠ADB+∠EDF=90°,根据∠CDF=∠ADB得∠F=∠EDF,从而得证;
(2)由![]() 可设EC=3,则EF=5,CF=8,证△EDC~△EBD得
可设EC=3,则EF=5,CF=8,证△EDC~△EBD得![]() ,据此知
,据此知![]() ,
,![]() ,BC=
,BC=![]() ,连接OB,OC,AC,AO并延长AO交BC于点H,由AB=AC,OB=OC知AO垂直平分BC,从而得
,连接OB,OC,AC,AO并延长AO交BC于点H,由AB=AC,OB=OC知AO垂直平分BC,从而得![]() ,再由AH⊥BC,DC⊥BC知DC∥AH,得
,再由AH⊥BC,DC⊥BC知DC∥AH,得![]() .
.
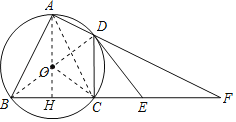
解:(1)连接BD,
∵AB=AC,
∴∠ABC=∠ADB,
∵∠ABC+∠ADC=180°,∠CDF+∠ADC=180°,
∴∠ABC=∠CDF,
∴∠CDF=∠ADB.
∵∠BAD=90°,
∴BD为⊙O的直径,
∴∠DCB=90°,
∴∠DCF=90°,
∴∠F+∠CDF=90°,
∵DE为⊙O的切线,
∴∠ODE=90°,
∴∠ADB+∠EDF=90°,
∵∠CDF=∠ADB,
∴∠F=∠EDF,
∴DE=EF;
(2)∵![]() ,
,
设EC=3,则EF=5,CF=3+5=8,
∵∠BDE=∠DCE=90°,∠DEC=∠DEB,
∴△EDC~△EBD,
∴![]() ,
,
∴![]() ,
,![]() ,,
,,
∴![]() ,
,
连接OB,OC,AC,AO并延长AO交BC于点H,
又∵OB=OC,AB=AC,
∴AO垂直平分BC,
∴![]() ,
,
∵AH⊥BC,DC⊥BC,
∴DC∥AH,
∴![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
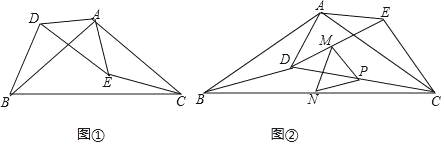
【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:

(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
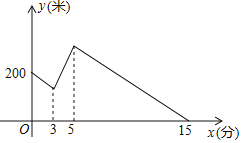
【题目】甲、乙两人分别从各自家出发乘坐出租车前往智博会,由于堵车,两人同时选择就近下车,已知甲车在乙车前面200米的A地下车,然后分别以各自的速度匀速走向会场,3分钟后,乙发现有物品遗落在出租车上,于是立即以不变的速度返回寻找,找到出租车时,出租车恰好向会场方向行驶了100米,乙拿到物品后立即以原速返回继续走向会场,同时甲以先前速度的一半走向会场,又经过10分钟,乙在B地追上甲,两人随后一起以甲放慢后的速度行走1分钟到达会场,甲、乙两人相距的路程y(m)与甲行走的时间x(min)之间的关系如图所示,(乙拿物品的时间忽略不计),则A地距离智博会会场的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是: ;
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于4的概率(请用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AC平分∠BAD,∠ABC=60°,E为AD上一点,AE=2,DE=4,P为AC 上一点,则△PDE周长的最小值为_______.
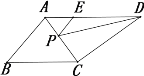
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的三个顶点A,B,D在坐标轴上,且已知点A(![]() ,
,![]() ),点B(
),点B(![]() ,
,![]() ),现有抛物线m经过点B,C和OD的中点.
),现有抛物线m经过点B,C和OD的中点.
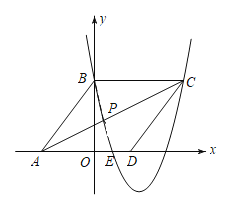
(1)求抛物线m的解析式;
(2)在抛物线![]() 上是否存在点P,使得
上是否存在点P,使得![]() ?若存在,求出点P的坐标,若不存在,请说明理由;
?若存在,求出点P的坐标,若不存在,请说明理由;
(3)抛物线m与x轴的另一交点为F,M是线段AC上一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
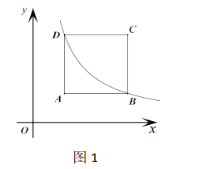
【题目】正方形![]() 的顶点
的顶点![]() ,点
,点![]() ,反比例函数
,反比例函数![]()
(1)如图1,双曲线经过点![]() 时求反比例函数
时求反比例函数![]() 的关系式;
的关系式;
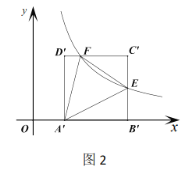
(2)如图2,正方形![]() 向下平移得到正方形
向下平移得到正方形![]() 边
边![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 的图象分别交正方形
的图象分别交正方形![]() 的边
的边![]() 、边
、边![]() 于点
于点![]()
①求![]() 的面积;
的面积;
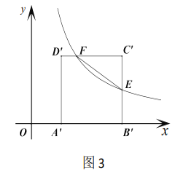
②如图3,![]() 轴上一点
轴上一点![]() ,是否存在
,是否存在![]() 是等腰三角形,若存在直接写出点
是等腰三角形,若存在直接写出点![]() 坐标,若不存在请说明理由.
坐标,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com