
 |
| AB |
| 3 |
| 3 |
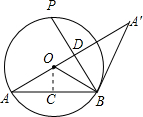 ∠AOB=120°,OA=OB,
∠AOB=120°,OA=OB,| 1 |
| 2 |
| 3 |
| 3 |
| 3 |


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在一个4×4的正方形网格中,现将其中的两个小正方形涂上阴影,请你用两种不同的方法分别在图中再将两个空白的小正方形涂上阴影,使它关于某点成中心对称,并用字母标出对称中心.
如图,在一个4×4的正方形网格中,现将其中的两个小正方形涂上阴影,请你用两种不同的方法分别在图中再将两个空白的小正方形涂上阴影,使它关于某点成中心对称,并用字母标出对称中心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com