
分析 (1)先去中括号,再去小括号然后移项后把x的系数化为1即可;
(2)根据分式的性质化简方程,再按照解方程的步骤解方程即可.
解答 解:(1)$\frac{1}{2}$[x-$\frac{1}{2}$(x-1)]=$\frac{2}{3}$(x+2),
$\frac{1}{2}$x-$\frac{1}{4}$(x-1)=$\frac{2}{3}$x+$\frac{4}{3}$,
$\frac{1}{2}$x-$\frac{1}{4}$x+$\frac{1}{4}$=$\frac{2}{3}$x+$\frac{4}{3}$,
6x-3x+3=8x+16,
∴x=-$\frac{13}{5}$;
(2)7+$\frac{0.3x-0.2}{0.2}$=$\frac{1.5-5x}{0.5}$.
整理得:70+15x-10=30-100x,
∴115x=30,
∴x=$\frac{6}{23}$.
点评 本题考查了解一元一次方程:去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a形式转化.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
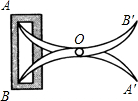 如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等..
如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com