
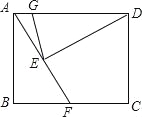
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,则![]() 的长为 .
的长为 .
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分:
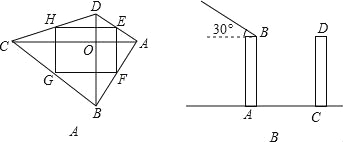
A.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点,若四边形EFGH的面积12,则四边形ABCD的面积为 .
B.如图,AB、CD是两栋楼,且AB=CD=30m,两楼间距AC=24m,当太阳光与水平线的夹角为30°时,AB楼在CD楼上的影子是 m.(精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
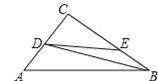
【题目】如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
(1)求证:DF⊥AB;
(2)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.

查看答案和解析>>
科目:初中数学 来源: 题型:
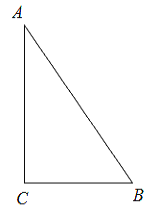
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长;
(2)问t满足什么条件时,△BCP为直角三角形;
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖
B.一组数据6,8,7,9,7,10的众数和中位数都是7
C.为了解全国中学生的心理健康情况,应该采用全面调查的方式
D.若甲乙两人六次跳远成绩的方差S![]() =0.1,S
=0.1,S![]() =0.03,则乙的成绩更稳定
=0.03,则乙的成绩更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲 乙两人在相同的条件下各射靶10次,射击成绩的平均数都是8环,甲射击成绩的方差是1.2,乙射击成绩的方差是1.8.下列说法中不一定正确的是( )
A. 甲、乙射击成绩的众数相同
B. 甲射击成绩比乙稳定
C. 乙射击成绩的波动比甲较大
D. 甲、乙射中的总环数相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C﹣A﹣B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为t(s)(0<t<8).
(1)求AB的长;
(2)当△BDE是直角三角形时,求t的值;
(3)设△CDE的面积为y(cm2),求y与t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com