
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分:
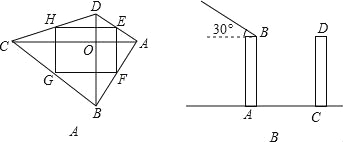
A.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点,若四边形EFGH的面积12,则四边形ABCD的面积为 .
B.如图,AB、CD是两栋楼,且AB=CD=30m,两楼间距AC=24m,当太阳光与水平线的夹角为30°时,AB楼在CD楼上的影子是 m.(精确到0.1m)
【答案】A、24;B、16.1.
【解析】
试题分析:A、∵点E、F、G、H分别为边AD、AB、BC、CD的中点,
∴HG是△DBC的中位线,
∴GH∥BD,
∴△CHG∽△BDC,
∴S△CHG=![]() S△BDC,
S△BDC,
同理S△AEF=![]() S△ADB,
S△ADB,
∴S△CHG+S△AEF=![]() S△BDC+
S△BDC+![]() S△ADB=
S△ADB=![]() S四边形ABCD,
S四边形ABCD,
同理S△DEH+S△BFG=![]() S四边形ABCD,
S四边形ABCD,
∴S△CHG+S△AEF+S△DEH+S△BFG,
=![]() S四边形ABCD+
S四边形ABCD+![]() S四边形ABCD,
S四边形ABCD,
=![]() S四边形ABCD,
S四边形ABCD,
∴S四边形ABCD=2S四边形EFGH=2×12=24;
故答案为:24.
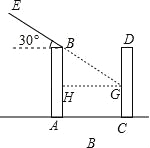
B、延长EA交CD于G,过G作GH⊥AB于H,
∵太阳光与水平线的夹角为30°,
∴∠AGH=30°,
∵BC=GH=24,
在Rt△AHG中,tan30°=![]() ,
,
∴AH=24×tan30°=24×![]() =8
=8![]() ,
,
∴CG=BH=AB﹣BH=30﹣8![]() =30﹣8×1.732≈16.1,
=30﹣8×1.732≈16.1,
故答案为:16.1.


科目:初中数学 来源: 题型:
【题目】李钰同学利用计算机设计了一个程序,输入和输出的数据如下表:
输入 | … | 1 | 2 | 3 | 4 | 5 | … |
输出 | … | 2 | 5 | 10 | 17 | 26 | … |
那么,当输入数据8时,输出的数据是( )
A. 61 B. 63 C. 65 D. 67
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:①若a>b,则ac2>bc2;②若ab>c,则b>![]() ;③若-3a>2a,则a<0;④若a<b,则a-c<b-c,其中正确命题的序号是 ( )
;③若-3a>2a,则a<0;④若a<b,则a-c<b-c,其中正确命题的序号是 ( )
A.③④
B.①③
C.①②
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在△ABC中,D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)求∠AFC的度数;
(2)求∠EDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,然后解答提出的问题:
设a,b是有理数,且满足a+![]() b=3﹣2
b=3﹣2![]() ,求ba的值.
,求ba的值.
解:由题意得(a﹣3)+(b+2)![]() =0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,
=0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,
由于![]() 是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+
是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+![]() y=8+4
y=8+4![]() ,求x+y的值.
,求x+y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次国际乒乓球单打比赛中,甲、乙两名中国选手进入最后决赛,那么下列事件为必然事件的是( )
A. 冠军属于中国选手 B. 冠军属于外国选手
C. 冠军属于中国选手甲 D. 冠军属于中国选手乙
查看答案和解析>>
科目:初中数学 来源: 题型:
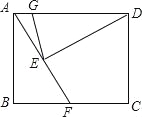
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,则![]() 的长为 .
的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com