
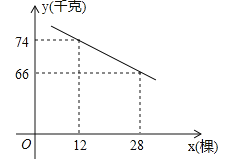
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
【答案】(1)y=﹣0.5x+80;(2)10;(3)当增种果树40棵时果园的最大产量是7200千克.
【解析】
试题分析:(1)函数的表达式为y=kx+b,把点(12,74),(28,66)代入解方程组即可.
(2)列出方程解方程组,再根据实际意义确定x的值.
(3)构建二次函数,利用二次函数性质解决问题.
试题解析:(1)设函数的表达式为y=kx+b,该一次函数过点(12,74),(28,66),得:![]() ,解得:
,解得:![]() ,∴该函数的表达式为y=﹣0.5x+80;
,∴该函数的表达式为y=﹣0.5x+80;
(2)根据题意,得,(﹣0.5x+80)(80+x)=6750,解得,![]() =10,
=10,![]() =70.
=70.
∵投入成本最低,∴![]() =70不满足题意,舍去,∴增种果树10棵时,果园可以收获果实6750千克.
=70不满足题意,舍去,∴增种果树10棵时,果园可以收获果实6750千克.
(3)根据题意,得:
w=(﹣0.5x+80)(80+x)=![]() ,∵a=﹣0.5<0,则抛物线开口向下,函数有最大值,∴当x=40时,w最大值为7200千克,∴当增种果树40棵时果园的最大产量是7200千克.
,∵a=﹣0.5<0,则抛物线开口向下,函数有最大值,∴当x=40时,w最大值为7200千克,∴当增种果树40棵时果园的最大产量是7200千克.


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为 x ( x 大于0)秒.![]()
(1)点C表示的数是;
(2)当 ![]() 秒时,点P到达点A处?
秒时,点P到达点A处?
(3)运动过程中点P表示的数是(用含字母 ![]() 的式子表示);
的式子表示);
(4)当P,C之间的距离为2个单位长度时,求 x 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.0000105m,该数值用科学记数法表示为( )
A.1.05×105
B.1.05×10﹣5
C.0.105×10﹣5
D.10.5×10﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤进行裁剪和拼图.
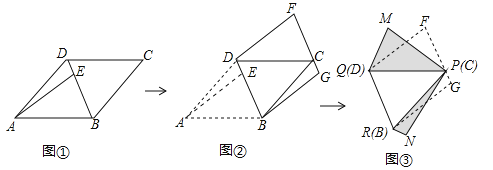
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com