
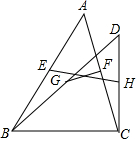
 如图,同底边BC的△ABC与△DBC中,E、F、G、H分别是AB、AC、DB、DC的中点,求证:EH与FG互相平分.
如图,同底边BC的△ABC与△DBC中,E、F、G、H分别是AB、AC、DB、DC的中点,求证:EH与FG互相平分. 分析 要证明EF和GH互相平分,只需构造一个平行四边形,运用平行四边形的性质:平行四边形的对角线互相平分即可证明.
解答 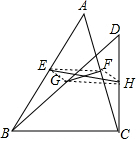 证明:连接EG、GF、FH、HE,
证明:连接EG、GF、FH、HE,
∵点E、F、G、H分别是AB、CD、AC、BD的中点,
∴EF、GH分别是△ABC与△DBC的中位线,
∴EF$\stackrel{∥}{=}$$\frac{1}{2}$BC,GH$\stackrel{∥}{=}$$\frac{1}{2}$BC,
∴EF$\stackrel{∥}{=}$GH.
∴四边形EGFH为平行四边形.
∴EF与GH互相平分.
点评 本题考查的是综合运用平行四边形的性质和判定定理.熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
 在河岸L的同侧有A、B两村,现拟在河岸边修建一座水泵站P,要求使管道PA、PB所用的水管最短,另修一码头Q,要求码头到A、B两村的距离相等,试画出P、Q所在的位置.
在河岸L的同侧有A、B两村,现拟在河岸边修建一座水泵站P,要求使管道PA、PB所用的水管最短,另修一码头Q,要求码头到A、B两村的距离相等,试画出P、Q所在的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com