
【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=![]() ,求AB的长;
,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=![]() AF.
AF.

【答案】(1)AB=6;(2)证明见解析.
【解析】
(1)设BM=x,则CM=2x,BC=BA=3x;在Rt△ABM中,E为斜边AM中点,根据直角三角形斜边的中线等于斜边的一半可得AM=2BE=2![]() .由勾股定理可得AM2=MB2+AB2,即可得40=x2+9x2,解得x=2.所以AB=3x=6;(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.证明△ABF≌△ADH,根据全等三角形的性质可得AF=AH,BF=DH.再由Rt△FAH是等腰直角三角形,可得HF=
.由勾股定理可得AM2=MB2+AB2,即可得40=x2+9x2,解得x=2.所以AB=3x=6;(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.证明△ABF≌△ADH,根据全等三角形的性质可得AF=AH,BF=DH.再由Rt△FAH是等腰直角三角形,可得HF=![]() AF.由HF=DH+DF=BF+DF,可得BF+DF=
AF.由HF=DH+DF=BF+DF,可得BF+DF=![]() AF.
AF.
解:(1)设BM=x,则CM=2x,BC=3x,
∵BA=BC,
∴BA=3x.
在Rt△ABM中,E为斜边AM中点,
∴AM=2BE=2![]() .
.
由勾股定理可得AM2=MB2+AB2,
即40=x2+9x2,解得x=2.
∴AB=3x=6.
(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.

∵DF平分∠CDE,
∴∠1=∠2.
∵DE=DA,DP⊥AF
∴∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
∴∠DFP=90°﹣45°=45°.
∴AH=AF.
∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,
∴∠BAF=∠DAH.
又AB=AD,
∴△ABF≌△ADH(SAS).
∴AF=AH,BF=DH.
∵Rt△FAH是等腰直角三角形,
∴HF=![]() AF.
AF.
∵HF=DH+DF=BF+DF,
∴BF+DF=![]() AF.
AF.


科目:初中数学 来源: 题型:
【题目】已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
(1)如图1,∠BME,∠E,∠END的数量关系为 (直接写出答案);
(2)如图2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度数(用用含m的式子表示)
(3)如图3,点G为CD上一点,∠BMN=n·∠EMN,∠GEK=n·∠GEM,EH∥MN交AB于点H,探究∠GEK,∠BMN,∠GEH之间的数量关系(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若一个整数能表示成a2+b2(a、b是整数)的形式,则称这个数为“平和数”,例如5是“平和数”,因为5=22+1,再如,M=x2+2xy+2y2=(x+y)2+y2(x,y是整数),我们称M也是“平和数”.
(1)请你写一个小于5的“平和数”,并判断34是否为“平和数”.
(2)已知S=x2+9y2+6x﹣6y+k(x,y是整数,k是常数,要使S为“平和数”,试求出符合条件的一个k值,并说明理由.
(3)如果数m,n都是“平和数”,试说明![]() 也是“平和数”.
也是“平和数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 是
是![]() 的中线,
的中线,![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() .
.
(1)如图1,求证:四边形![]() 是平行四边形;
是平行四边形;


(2)如图2,若![]() ,请直接写出图中所有的等腰三角形,不需要证明.
,请直接写出图中所有的等腰三角形,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰ΔABC中,∠CAB=90°AB=AC,P为ΔABC内的一点,且PA=AQ=1,CQ=BP=3,CP=![]() ,求∠APC的大小.(提示:连接PQ)
,求∠APC的大小.(提示:连接PQ)
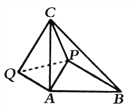
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC边长为20,点D的坐标为(![]() ,0),且
,0),且![]() 以OD、DE为邻边作长方形ODEF.
以OD、DE为邻边作长方形ODEF.
(1)请直接写出以下点的坐标:E_____,F______ (用含![]() 的式子表示);
的式子表示);
(2)设长方形ODEF与正方形OABC重叠部分面积为S,求S(用含![]() 的式子表示);
的式子表示);
(3)S的值能否等于300,若能请求出此时![]() 的值;若不能,请说明理由。
的值;若不能,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在平行四边形![]() 内作一个菱形.甲,乙两位同学的作法分别如下:
内作一个菱形.甲,乙两位同学的作法分别如下:

对于甲乙两人的作法,可判断( )
A.甲正确,乙错误B.甲错误,乙正确C.甲,乙均正确D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(-2,2),第四次向右跳动5个单位至点A4(3,2),………,依此规律跳动下去,点A第100次跳动至点A100的坐标是________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com