
【题目】如图,在等腰ΔABC中,∠CAB=90°AB=AC,P为ΔABC内的一点,且PA=AQ=1,CQ=BP=3,CP=![]() ,求∠APC的大小.(提示:连接PQ)
,求∠APC的大小.(提示:连接PQ)
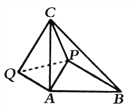
【答案】135°.
【解析】
试题由于△ABC为等腰直角三角形,AB=AC,则把△APB绕A点逆时针旋转90°可得到△AQC,连PQ,根据旋转的性质得到∠QAP=90°,QA=PA=1,QC=PB=3,得到△PAQ为等腰直角三角形,根据等腰直角三角形的性质得QP=![]() PA=
PA=![]() ,∠APQ=45°,在△QPC中,可得到PC2+QP2=QC2,根据勾股定理的逆定理得到△QPC为直角三角形,∠CPQ=90°,利用∠CPA=∠CPQ+∠APP′进行计算即可.
,∠APQ=45°,在△QPC中,可得到PC2+QP2=QC2,根据勾股定理的逆定理得到△QPC为直角三角形,∠CPQ=90°,利用∠CPA=∠CPQ+∠APP′进行计算即可.
试题解析:∵△ABC为等腰直角三角形,AB=AC,
∴把△APB绕A点逆时针旋转90°可得到△AQC,连PQ,如图,

∴∠QAP=90°,QA=PA=1,QC=PB=3,
∴△PAQ为等腰直角三角形,
∴QP=![]() PA=
PA=![]() ,∠APQ=45°,
,∠APQ=45°,
在△QPC中,QC=3,QP=![]() ,PC=
,PC=![]() ,
,
∵(![]() )2+(
)2+(![]() )2=32,
)2=32,
∴PC2+QP2=QC2,
∴△QPC为直角三角形,∠CPQ=90°,
∴∠CPA=∠CPQ+∠APQ=90°+45°=135°.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E. 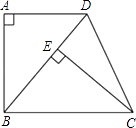
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3 ![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC;②∠EDA=∠B;③OA= ![]() AC;④DE是⊙O的切线,正确的个数是( )
AC;④DE是⊙O的切线,正确的个数是( )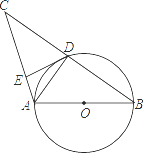
A.1 个
B.2个
C.3 个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=![]() ,求AB的长;
,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=![]() AF.
AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在行驶完某段全程600千米的高速公路时,李师傅对张师傅说:“你的车速太快了,平均每小时比我多跑20千米,比我少用1.5小时就跑完了全程.”
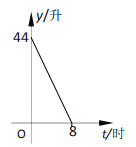
(1)若这段高速公路全程限速120千米/小时,两人全程均匀速行驶.那么张师傅超速了吗?请说明理由;
(2)张师傅所行驶的车内油箱余油量![]() (升)与行驶时间
(升)与行驶时间![]() (时)的函数关系如图所示,则行驶完这段高速公路,他至少需要多少升油?
(时)的函数关系如图所示,则行驶完这段高速公路,他至少需要多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
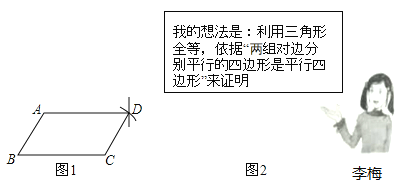
【题目】李梅同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形![]() ,并写出了如下不完整的已知和求证.
,并写出了如下不完整的已知和求证.
已知:如图1,在四边形![]() 中,
中,![]() ,
,![]()
求证:四边形![]() 是 四边形.
是 四边形.
(1)填空,补全已知和求证;
(2)按李梅的想法写出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请先阅读下列材料,再解答下列问题:
材料:因式分解:(x y)22(x y)1 .
解:将“ x y”看成整体,令 x y=A ,则
原式 A2A 1 ( A 1)2
再将“A”还原,得:原式 (x y 1)2 . 上述解题时用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法,请你解答下列问题:
(1)因式分解:(x y)26(x y) 9 = ;
(2)因式分解:(a b)(a b 4) 4 ;
(3)证明:若 n 为正整数,则式子(n 1)(n 2)(n23n) 1 的值一定是某一个整数的平方.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com