
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E. 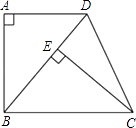
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
【答案】
(1)证明:∵AD∥BC,
∴∠ADB=∠EBC.
∵CE⊥BD,∠A=90°,
∴∠A=∠CEB,
在△ABD和△ECB中,
∵∠A=∠CEB,AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠BCE,
又∵BC=BD
∴△ABD≌△ECB
(2)解:∵∠DBC=50°,BC=BD,
∴∠EDC= ![]() (180°﹣50°)=65°,
(180°﹣50°)=65°,
又∵CE⊥BD,
∴∠CED=90°,
∴∠DCE=90°﹣∠EDC=90°﹣65°=25°.
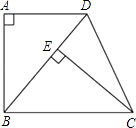
【解析】(1)因为这两个三角形是直角三角形,BC=BD,因为AD∥BC,还能推出∠ADB=∠EBC,从而能证明:△ABD≌△ECB.(2)因为∠DBC=50°,BC=BD,可求出∠BDC的度数,进而求出∠DCE的度数.
【考点精析】关于本题考查的直角梯形,需要了解一腰垂直于底的梯形是直角梯形才能得出正确答案.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】A、B、C、D、E、F六个球队进行单循环比赛(每两队之间赛一场,比赛结果必须分出胜负),每天同时在三个场地各进行一场比赛,前四天的积分表如下(E、F的积分被遮挡):
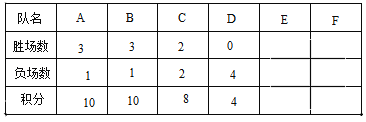
(1)根据积分榜,胜一场积几分,负一场积几分?
(2)若E队前四天积分比F队多4分,问E、F两队前四天的战绩分别是几胜几负?
(3)已知第一天B与D对阵,第二天C与E对阵,第三天D与F对阵,第四天B与C对阵,试分析第五天A和谁对阵比赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表![]() 单位:环
单位:环![]() :
:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
甲 | 10 | 9 | 8 | 8 | 10 | 9 |
乙 | 10 | 10 | 8 | 10 | 7 | 9 |
根据表格中的数据,可计算出甲、乙两人的平均成绩都是9环.
(1)分别计算甲、乙六次测试成绩的方差;
(2)根据数据分析的知识,你认为选______名队员参赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
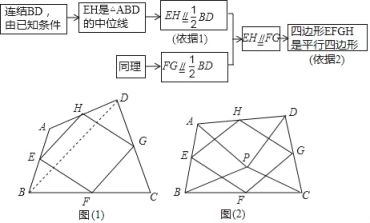
问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.试说明中点四边形EFGH是平行四边形.
探究展示:勤奋小组的解题思路:
反思交流:
(1)①上述解题思路中的“依据1”、“依据2”分别是什么?
依据1: ;依据2: ;
②连接AC,若AC=BD时,则中点四边形EFGH的形状为 ;
创新小组受到勤奋小组的启发,继续探究:
(2)如图(2),点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并说明理由;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
(1)如图1,∠BME,∠E,∠END的数量关系为 (直接写出答案);
(2)如图2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度数(用用含m的式子表示)
(3)如图3,点G为CD上一点,∠BMN=n·∠EMN,∠GEK=n·∠GEM,EH∥MN交AB于点H,探究∠GEK,∠BMN,∠GEH之间的数量关系(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一条输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.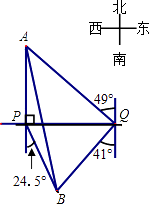
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题: 如图1,在矩形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,连接所
的中点,连接所![]() 、
、![]() 、
、![]() .
.
求证:![]() 是等边三角形.
是等边三角形.
小明经探究发现,连接![]() 、
、![]() (如图2),从而可证
(如图2),从而可证![]() ,
, ![]() ,使问题得到解决.
,使问题得到解决.

(1)请你按照小明的探究思路,完成他的证明过程;
参考小明思考问题的方法或用其他的方法,解决下面的问题:
(2)如图3,在四边形![]() 中,
中, ![]() ,
,![]() , 对角线
, 对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() (
(![]() ),点
),点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() 、
、![]() .
.
①否存在与![]() 相等的线段?若存在,请找出并证明;若不存在,说明理由.
相等的线段?若存在,请找出并证明;若不存在,说明理由.
②求![]() 的度数.(用含
的度数.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
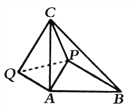
【题目】如图,在等腰ΔABC中,∠CAB=90°AB=AC,P为ΔABC内的一点,且PA=AQ=1,CQ=BP=3,CP=![]() ,求∠APC的大小.(提示:连接PQ)
,求∠APC的大小.(提示:连接PQ)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com