
ΓΨΧβΡΩΓΩΉέΚœ”κ ΒΦυ
Έ Χβ«ιΨ≥ΘΚ‘Ύ ΐ―ßΜνΕ·ΩΈ…œΘ§Έ“Ο«Ηχ≥ω»γœ¬Ε®“εΘΚΥ≥¥ΈΝ§Α¥»Έ“β“ΜΗωΥΡ±Ώ–ΈΗς±Ώ÷–ΒψΥυΒΟΒΡΥΡ±Ώ–ΈΫ–÷–ΒψΥΡ±Ώ–ΈΘ°»γΆΦΘ®1Θ©Θ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ΒψEΘ§FΘ§GΘ§HΖ÷±πΈΣ±ΏABΘ§BCΘ§CDΘ§DAΒΡ÷–ΒψΘ° ‘ΥΒΟς÷–ΒψΥΡ±Ώ–ΈEFGH «ΤΫ––ΥΡ±Ώ–ΈΘ°
ΧΫΨΩ’Ι ΨΘΚ«ΎΖή–ΓΉιΒΡΫβΧβΥΦ¬ΖΘΚ
Ζ¥ΥΦΫΜΝςΘΚ
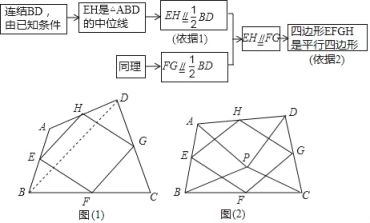
Θ®1Θ©ΔΌ…œ ωΫβΧβΥΦ¬Ζ÷–ΒΡΓΑ“άΨί1Γ±ΓΔΓΑ“άΨί2Γ±Ζ÷±π « ≤Ο¥ΘΩ
“άΨί1ΘΚΓΓ ΓΓΘΜ“άΨί2ΘΚΓΓ ΓΓΘΜ
ΔΎΝ§Ϋ”ACΘ§»τACΘΫBD ±Θ§‘ρ÷–ΒψΥΡ±Ώ–ΈEFGHΒΡ–ΈΉ¥ΈΣΓΓ ΓΓΘΜ
¥¥–¬–ΓΉι ήΒΫ«ΎΖή–ΓΉιΒΡΤτΖΔΘ§ΦΧ–χΧΫΨΩΘΚ
Θ®2Θ©»γΆΦΘ®2Θ©Θ§ΒψP «ΥΡ±Ώ–ΈABCDΡΎ“ΜΒψΘ§«“¬ζΉψPAΘΫPBΘ§PCΘΫPDΘ§ΓœAPBΘΫΓœCPDΘ§ΒψEΘ§FΘ§GΘ§HΖ÷±πΈΣ±ΏABΘ§BCΘ§CDΘ§DAΒΡ÷–ΒψΘ§≤¬œκ÷–ΒψΥΡ±Ώ–ΈEFGHΒΡ–ΈΉ¥Θ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©»τΗΡ±δΘ®2Θ©÷–ΒΡΧθΦΰΘ§ ΙΓœAPBΘΫΓœCPDΘΫ90ΓψΘ§ΤδΥϋΧθΦΰ≤Μ±δΘ§‘ρ÷–ΒψΥΡ±Ώ–ΈEFGHΒΡ–ΈΉ¥ΈΣΓΓ ΓΓΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ“άΨί1ΘΚ»ΐΫ«–ΈΒΡ÷–ΈΜœΏΕ®άμΘ°“άΨί2ΘΚ“ΜΉιΕ‘±ΏΤΫ––«“œύΒ»ΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ°ΔΎΝβ–ΈΘ°άμ”…ΦϊΫβΈωΘΜΘ®2Θ©ΥΡ±Ώ–ΈEFGH «Νβ–ΈΘ°άμ”…ΦϊΫβΈωΘΜΘ®3Θ©’ΐΖΫ–ΈΘ°άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί»ΐΫ«–Έ÷–ΈΜœΏΕ®άμΫβ¥πΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ≈–Ε®ΚΆΝβ–ΈΒΡ≈–Ε®Ϋβ¥πΦ¥Ω…Θ°
Θ®3Θ©ΗυΨί”–“ΜΗωΫ« «÷±Ϋ«ΒΡΝβ–Έ «’ΐΖΫ–ΈΦ¥Ω…÷ΛΟςΘ°
Θ®1Θ©ΔΌ“άΨί1ΘΚ»ΐΫ«–ΈΒΡ÷–ΈΜœΏΕ®άμΘ°
“άΨί2ΘΚ“ΜΉιΕ‘±ΏΤΫ––«“œύΒ»ΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ°
ΔΎΝβ–ΈΘ°
άμ”…ΘΚ»γΆΦ1÷–Θ§
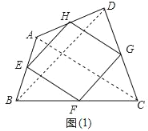
ΓΏAEΘΫBEΘ§AHΘΫHDΘ§
ΓύEHΘΫ![]() BDΘ§
BDȧ
ΓΏDHΘΫHAΘ§DGΘΫGCΘ§
ΓύHGΘΫ![]() ACΘ§
ACȧ
ΓύHEΘΫHGΘ§
ΓΏΥΡ±Ώ–ΈEFGH «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύΥΡ±Ώ–ΈEFGH «Νβ–ΈΘ°
Ι ¥πΑΗΈΣ»ΐΫ«–Έ÷–ΈΜœΏΕ®άμΘ§“ΜΉιΕ‘±ΏΤΫ––«“œύΒ»ΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ§Νβ–ΈΘ°
Θ®2Θ©Ϋα¬έΘΚΥΡ±Ώ–ΈEFGH «Νβ–ΈΘ°
άμ”…ΘΚ»γΆΦ2÷–Θ§Ν§Ϋ”ACΘ§BD
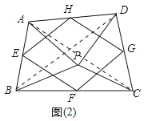
ΓΏΓœAPBΘΫΓœCPD
ΓύΓœAPB+ΓœAPDΘΫΓœCPD+ΓœAPD
Φ¥ΘΚΓœBPDΘΫΓœAPC
ΓΏPAΘΫPBΘ§PCΘΫPD
ΓύΓςAPCΓ’ΓςBPD
ΓύACΘΫBD
ΓύHGΘΫHE
”…(1)Ω…÷ΣΘΚΥΡ±Ώ–ΈEFGH «ΤΫ––ΥΡ±Ώ–Έ
ΓύΥΡ±Ώ–ΈEFGH «Νβ–ΈΘ°
Θ®3Θ©Ϋα¬έΘΚ’ΐΖΫ–ΈΘ°
άμ”…ΘΚ»γΆΦ2©¹1÷–Θ§Ν§Ϋ”ACΘ§BDΘ§BDΫΜAC”ΎΒψOΘ§ΫΜGH”ΎΒψKΘ§ACΫΜPD”ΎΒψJΘ°
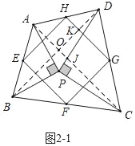
ΓΏΓςAPCΓ’ΓςBPDΘ§ΓœDPCΘΫ90ΓψΘ§
ΓύΓœPDBΘΫΓœPCAΘ§
ΓΏΓœPJCΘΫΓœDJOΘ§
ΓύΓœCPJΘΫΓœDOJΘΫ90ΓψΘ§
ÿHGøACȧ
ΓύΓœBKGΘΫΓœBOCΘΫ90ΓψΘ§
ÿEHøBDȧ
ΓύΓœEHGΘΫΓœBKGΘΫ90ΓψΘ§
ΓΏΥΡ±Ώ–ΈEFGH «Νβ–ΈΘ§
ΓύΥΡ±Ώ–ΈEFGH «’ΐΖΫ–ΈΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB”κΓ―Oœύ«–”ΎΒψCΘ§OAΘ§OBΖ÷±πΫΜΓ―O”ΎΒψDΘ§EΘ§ ![]() =
= ![]()

Θ®1Θ©«σ÷ΛΘΚOA=OBΘΜ
Θ®2Θ©“―÷ΣAB=4 ![]() Θ§OA=4Θ§«σ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
Θ§OA=4Θ§«σ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
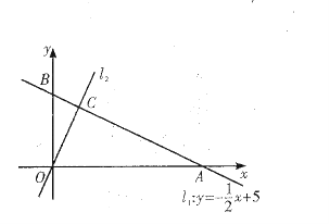
ΓΨΧβΡΩΓΩ÷±œΏAB”κx÷αΫΜ”ΎΒψAΘ®1Θ§0Θ©Θ§”κy÷αΫΜ”ΎΒψBΘ®0Θ§-2Θ©Θ°
Θ®1Θ©«σ÷±œΏABΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©»τ÷±œΏAB…œ”–“ΜΕ·ΒψCΘ§«“![]() Θ§«σΒψCΒΡΉχ±ξΘ°
Θ§«σΒψCΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–ΈABCD÷–Θ§ΓœA=ΓœC=90ΓψΘ§BEΤΫΖ÷ΓœABCΘ§DFΤΫΖ÷ΓœADCΘ§‘ρBE”κDF”–ΚΈΈΜ÷ΟΙΊœΒΘΩ ‘ΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABCΡΎΫ””ΎΓ―OΘ§ΓœB=60ΓψΘ§CD «Γ―OΒΡ÷±ΨΕΘ§ΒψP «CD―”≥ΛœΏ…œΒΡ“ΜΒψΘ§«“AP=ACΘ°
Θ®1Θ©«σ÷ΛΘΚPA «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©»τAB=4+ ![]() Θ§BC=2
Θ§BC=2 ![]() Θ§«σΓ―OΒΡΑκΨΕΘ°
Θ§«σΓ―OΒΡΑκΨΕΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥ‘ω«Ω―ß…ζΕ‘÷–ΜΣ”≈–ψ¥ΪΆ≥ΈΡΜ·ΒΡάμΫβΘ§ΨωΕ®ΙΚ¬ρ“Μ≈ζœύΙΊΒΡ ιΦ°Θ°ΨίΝΥΫβΘ§Ψ≠Βδ÷χΉςΒΡΒΞΦέ±»¥ΪΥΒΙ ¬ΒΡΒΞΦέΕύ6‘ΣΘ§”Ο10000‘ΣΙΚ¬ρΨ≠Βδ÷χΉς”κ”Ο7000‘ΣΙΚ¬ρ¥ΪΥΒΙ ¬ΒΡ±Ψ ΐœύΆ§Θ§’βΝΫάύ ιΦ°ΒΡΒΞΦέΗς «Εύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΥΡ±Ώ–ΈABCD «Χί–ΈΘ§ADΓΈBCΘ§ΓœA=90ΓψΘ§BC=BDΘ§CEΓΆBDΘ§¥ΙΉψΈΣEΘ° 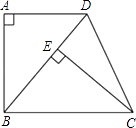
Θ®1Θ©«σ÷ΛΘΚΓςABDΓ’ΓςECBΘΜ
Θ®2Θ©»τΓœDBC=50ΓψΘ§«σΓœDCEΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§“Μ¥ΈΚ· ΐ
÷–Θ§“Μ¥ΈΚ· ΐ![]() ΒΡΆΦœσ
ΒΡΆΦœσ![]() Ζ÷±π”κ
Ζ÷±π”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΝΫΒψΘ§’ΐ±»άΐΚ· ΐΒΡΆΦœσ
ΝΫΒψΘ§’ΐ±»άΐΚ· ΐΒΡΆΦœσ![]() ”κ
”κ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]()
Θ®1Θ©«σ![]() ΒΡ÷ΒΦΑ
ΒΡ÷ΒΦΑ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©“Μ¥ΈΚ· ΐ![]() ΒΡΆΦœσΈΣ
ΒΡΆΦœσΈΣ![]() «“
«“![]() ≤ΜΡήΈß≥…»ΐΫ«–ΈΘ§÷±Ϋ”–¥≥ω
≤ΜΡήΈß≥…»ΐΫ«–ΈΘ§÷±Ϋ”–¥≥ω![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§Γ―OΫΜBCΒΡ÷–Βψ”ΎDΘ§DEΓΆAC”ΎEΘ§Ν§Ϋ”ADΘ§‘ρœ¬Ν–Ϋα¬έΘΚ
ΔΌADΓΆBCΘΜΔΎΓœEDA=ΓœBΘΜΔέOA= ![]() ACΘΜΔήDE «Γ―OΒΡ«–œΏΘ§’ΐ»ΖΒΡΗω ΐ «Θ® Θ©
ACΘΜΔήDE «Γ―OΒΡ«–œΏΘ§’ΐ»ΖΒΡΗω ΐ «Θ® Θ©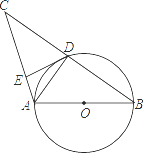
A.1 Ηω
B.2Ηω
C.3 Ηω
D.4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com