
【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E, ![]() =
= ![]()

(1)求证:OA=OB;
(2)已知AB=4 ![]() ,OA=4,求阴影部分的面积.
,OA=4,求阴影部分的面积.
【答案】
(1)解:连接OC,
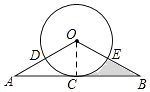
∵AB与⊙O相切于点C
∴∠ACO=90°,
由于 ![]() =
= ![]() ,
,
∴∠AOC=∠BOC,
∴∠A=∠B
∴OA=OB,
(2)解:由(1)可知:△OAB是等腰三角形,
∴BC= ![]() AB=2
AB=2 ![]() ,
,
∴sin∠COB= ![]() =
= ![]() ,
,
∴∠COB=60°,
∴∠B=30°,
∴OC= ![]() OB=2,
OB=2,
∴扇形OCE的面积为: ![]() =
= ![]() ,
,
△OCB的面积为: ![]() ×2
×2 ![]() ×2=2
×2=2 ![]()
∴S阴影=2 ![]() ﹣
﹣ ![]() π
π
【解析】(1)连接OC,由切线的性质可知∠ACO=90°,由于 ![]() =
= ![]() ,所以∠AOC=∠BOC,从而可证明∠A=∠B,从而可知OA=OB;(2)由(1)可知:△AOB是等腰三角形,所以AC=2
,所以∠AOC=∠BOC,从而可证明∠A=∠B,从而可知OA=OB;(2)由(1)可知:△AOB是等腰三角形,所以AC=2 ![]() ,从可求出扇形OCE的面积以及△OCB的面积
,从可求出扇形OCE的面积以及△OCB的面积
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】下列是用火柴棒拼成的一组图形,第①个图形中有 3 根火柴棒,第②个图形中有 9 根火柴棒,第③个图形中有 18 根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是( ).
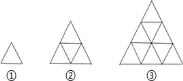
A. 63B. 60C. 56D. 45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠ABE与∠CDE的角平分线相交于点F,若∠F=125°,则∠E的度数为( )

A. 110° B. 120° C. 115° D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E. 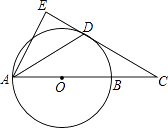
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3 ![]() ,求弦AD的长.
,求弦AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x﹣1)(x+1)= ;
(2)(x﹣1)(x2+x+1)= ;
(3)(x﹣1)(x3+x2+x+1)= ;
由此我们可以得到(x﹣1)(x99+x98+…+x+1)= ;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+…+2+1;
(2)(﹣3)50+(﹣3)49+…+(﹣3)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C、D、E、F六个球队进行单循环比赛(每两队之间赛一场,比赛结果必须分出胜负),每天同时在三个场地各进行一场比赛,前四天的积分表如下(E、F的积分被遮挡):
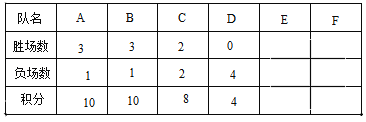
(1)根据积分榜,胜一场积几分,负一场积几分?
(2)若E队前四天积分比F队多4分,问E、F两队前四天的战绩分别是几胜几负?
(3)已知第一天B与D对阵,第二天C与E对阵,第三天D与F对阵,第四天B与C对阵,试分析第五天A和谁对阵比赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对某一区域进行绿化,安排甲.乙 两个工程队完成;已知甲队每天能完成绿化面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400![]() 区域的绿化时,甲队比乙队少用4天,求甲.乙两工程队每天能完成绿化的面积分别是多少
区域的绿化时,甲队比乙队少用4天,求甲.乙两工程队每天能完成绿化的面积分别是多少![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
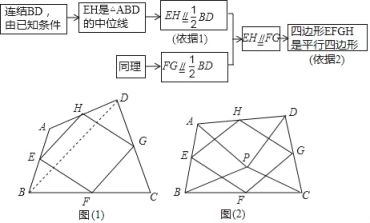
问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.试说明中点四边形EFGH是平行四边形.
探究展示:勤奋小组的解题思路:
反思交流:
(1)①上述解题思路中的“依据1”、“依据2”分别是什么?
依据1: ;依据2: ;
②连接AC,若AC=BD时,则中点四边形EFGH的形状为 ;
创新小组受到勤奋小组的启发,继续探究:
(2)如图(2),点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并说明理由;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com