
【题目】在行驶完某段全程600千米的高速公路时,李师傅对张师傅说:“你的车速太快了,平均每小时比我多跑20千米,比我少用1.5小时就跑完了全程.”
(1)若这段高速公路全程限速120千米/小时,两人全程均匀速行驶.那么张师傅超速了吗?请说明理由;
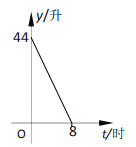
(2)张师傅所行驶的车内油箱余油量![]() (升)与行驶时间
(升)与行驶时间![]() (时)的函数关系如图所示,则行驶完这段高速公路,他至少需要多少升油?
(时)的函数关系如图所示,则行驶完这段高速公路,他至少需要多少升油?
科目:初中数学 来源: 题型:
【题目】如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一条输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.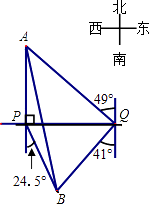
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() ,
, ![]() ,……,
,……, ![]() ,(n为正整数)
,(n为正整数)
(1)试说明![]() 是8的倍数;
是8的倍数;
(2)若△ABC的三条边长分别为![]() 、
、![]() 、
、![]() (
(![]() 为正整数)
为正整数)
①求![]() 的取值范围.
的取值范围.
②是否存在这样的![]() ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在⊙O的直径BA延长线上,PC与⊙O相切,切点为C,点D在⊙O上,连接PD、BD,已知PC=PD=BC.下列结论:
①PD与⊙O相切;
②四边形PCBD是菱形;
③PO=AB;
④∠PDB=120°.
其中,正确的个数是( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
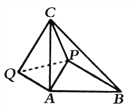
【题目】如图,在等腰ΔABC中,∠CAB=90°AB=AC,P为ΔABC内的一点,且PA=AQ=1,CQ=BP=3,CP=![]() ,求∠APC的大小.(提示:连接PQ)
,求∠APC的大小.(提示:连接PQ)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为3的正方形![]() 置于平面直角坐标系第一象限,使边
置于平面直角坐标系第一象限,使边![]() 落在
落在![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() :
:![]() 经过点
经过点![]() 且与
且与![]() 轴交于点
轴交于点![]() .
.

(1)求![]() 点坐标;
点坐标;
(2)求![]() 的面积;
的面积;
(3)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是直角三角形?若存在,请直接写出点
是直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,分别延长
的中点,分别延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
(2)如图2,连接![]() ,若
,若![]() 平分
平分![]() .
.
①求![]() 的长;
的长;
②如图3,连接![]() ,分别交
,分别交![]() 于点
于点![]() .求证:
.求证:![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com