
【题目】已知如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,分别延长
的中点,分别延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
(2)如图2,连接![]() ,若
,若![]() 平分
平分![]() .
.
①求![]() 的长;
的长;
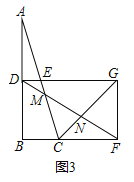
②如图3,连接![]() ,分别交
,分别交![]() 于点
于点![]() .求证:
.求证:![]() 是等腰三角形.
是等腰三角形.

【答案】(1)证明见解析;(2)①5;②证明见解析.
【解析】
(1)根据一组对边平行且相等可得:四边形DBFG是平行四边形,根据有一个角是直角的平行四边形是矩形可得结论;
(2)①如图2,过C作CH⊥DG于H,证明△ADE≌△CHE,得CH=AD,EH=DE,设CF=x,则BF=2+x,GH=CF=x,EG=x+1,根据平行线的性质和角平分线的定义得:EG=CG=x+1,结合勾股定理列方解方程可得结论;
②证明△DEM∽△FCM,得![]() 根据勾股定理计算AC、DF、CG的长,再结合
根据勾股定理计算AC、DF、CG的长,再结合![]() 可得MN=CM,得△MCN是等腰三角形.
可得MN=CM,得△MCN是等腰三角形.
证明:(1)如图1,∵点![]() 分别是
分别是![]() 的中点,
的中点,
![]()
![]()
![]()
∴四边形![]() 是平行四边形,
是平行四边形,
![]()
∴![]() 是矩形;
是矩形;
(2)①如图2,过![]() 作
作![]() 于
于![]() ,
,
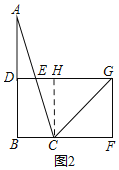
![]()
![]() ,
,
![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() 平分
平分![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
![]()
![]()
![]()
②如图![]() :
: ![]() ,
,
![]()
![]() ,
,
由勾股定理得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
同理得:![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰三角形.
是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象
的图象![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点,正比例函数的图象
两点,正比例函数的图象![]() 与
与![]() 交于点
交于点![]()
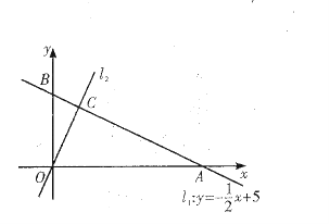
(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函数![]() 的图象为
的图象为![]() 且
且![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC;②∠EDA=∠B;③OA= ![]() AC;④DE是⊙O的切线,正确的个数是( )
AC;④DE是⊙O的切线,正确的个数是( )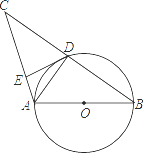
A.1 个
B.2个
C.3 个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在行驶完某段全程600千米的高速公路时,李师傅对张师傅说:“你的车速太快了,平均每小时比我多跑20千米,比我少用1.5小时就跑完了全程.”
(1)若这段高速公路全程限速120千米/小时,两人全程均匀速行驶.那么张师傅超速了吗?请说明理由;
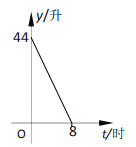
(2)张师傅所行驶的车内油箱余油量![]() (升)与行驶时间
(升)与行驶时间![]() (时)的函数关系如图所示,则行驶完这段高速公路,他至少需要多少升油?
(时)的函数关系如图所示,则行驶完这段高速公路,他至少需要多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
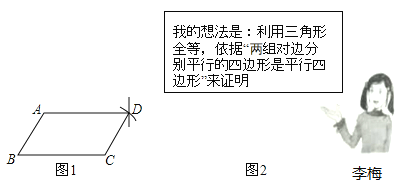
【题目】李梅同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形![]() ,并写出了如下不完整的已知和求证.
,并写出了如下不完整的已知和求证.
已知:如图1,在四边形![]() 中,
中,![]() ,
,![]()
求证:四边形![]() 是 四边形.
是 四边形.
(1)填空,补全已知和求证;
(2)按李梅的想法写出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级45名同学自发筹集到1700元资金,用于初中毕业时各项活动的经费.通过商议,决定拿出不少于544元但不超过560元的资金用于请专业人士拍照,其余资金用于给每名同学购买一件文化衫或一本制作精美的相册作为纪念品.已知每件文化衫28元,每本相册20元.
(1)适用于购买文化衫和相册的总费用为W元,求总费用W(元)与购买的文化衫件数t(件)的函数关系式.
(2)购买文化衫和相册有哪几种方案?为了使拍照的资金更充足,应选择哪种方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的数学作业本上都是等距的横线,相邻两条横线的距离都是1厘米,他把一个等腰直角三角板放ABC(∠ACB=90°,AC=BC)在本子上,点A、B、C恰好都在横线上,则斜边AB的长度为( )

A.10B.3![]() C.4
C.4![]() D.6
D.6![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com