
分析 设腰长为xcm,底为ycm,则可知2x+y=20+8,x+$\frac{1}{2}$x=20或9,可求得y.
解答 解:设腰长为xcm,底为ycm,
则由题意可知x+$\frac{1}{2}$x=20或8,解得x=$\frac{40}{3}$或$\frac{16}{3}$,
而三角形的周长为2x+y=20+8,
当x=$\frac{40}{3}$时可解得y=8,此时三角形的三边为$\frac{40}{3}$cm,$\frac{40}{3}$cm,8cm,满足三角形的三边关系,此时底边长为8cm,
当x=$\frac{16}{3}$时可解得y=$\frac{52}{3}$,此时三角形的三边为$\frac{16}{3}$cm,$\frac{16}{3}$cm,$\frac{52}{3}$cm,不满足三角形的三边关系,不合题意;
综上可知底边长8cm.
点评 本题主要考查等腰三角形的性质,由条件分两种情况求得三角形的各边长再利用三角形的三边关系进行验证是解题的关键,注意方程思想的应用.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
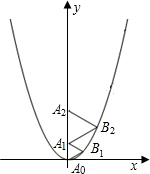 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com