
(本题满分8分)已知抛物线y= +kx+b经过点P(2,-3),Q(-1,0).
+kx+b经过点P(2,-3),Q(-1,0).

(1)求抛物线的解析式.
(2)设抛物线顶点为 ,与
,与 轴交点为
轴交点为 .求
.求 的值.
的值.
(3)设抛物线与 轴的另一个交点为
轴的另一个交点为 ,求四边形
,求四边形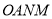 的面积.
的面积.
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源:[同步]2014年北师大版八年级上 2.4估算练习卷(解析版) 题型:?????
(2014•安徽模拟)在实数0,﹣ ,
, ,|﹣2|中,最小的是( )
,|﹣2|中,最小的是( )
A. B.﹣
B.﹣ C.0 D.|﹣2|
C.0 D.|﹣2|
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.

(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,ABCD是平行四边形,AB是☉O的直径,点D在☉O上,AD = OA =1, 则图中阴影部分的面积为( )

A. B.
B.
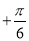 C.
C.
 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:解答题
(10分)如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个动点到达终点时,另一个动点也随之停止运动.

(1)求AC、BC的长;
(2)设点P的运动时间为x(秒),△PBQ的面积为y(cm2),当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;
(3)当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC是否相似,请说明理由;
(4)当x=5秒时,在直线PQ上是否存在一点M,使△BCM得周长最小,若存在,求出最小周长,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:填空题
已知二次函数y=ax2+bx+c与一次函数y=x的图象如图所示,给出以上结论:
①b2-4ac>0;②a+b+c=1;③当1<x<3时,ax2+(b-1)x+c<0;④二次函数y=ax2+(b-1)x+c的图象经过点(1,0)和(3,0).其中正确的有: (把你认为正确结论的序号都填上).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:解答题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
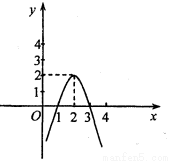
(1)写出y>0时,x的取值范围 ;
(2)写出y随x的增大而减小的自变量x的取值范围 ;
(3)求函数y=ax2+bx+c的表达式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c(a≠0)的图象如图,则函数值y>0时,x的取值范围是( )
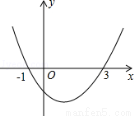
A.x<﹣1 B.x>3 C.﹣1<x<3 D.x<﹣1或x>3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com