
(10分)如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个动点到达终点时,另一个动点也随之停止运动.

(1)求AC、BC的长;
(2)设点P的运动时间为x(秒),△PBQ的面积为y(cm2),当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;
(3)当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC是否相似,请说明理由;
(4)当x=5秒时,在直线PQ上是否存在一点M,使△BCM得周长最小,若存在,求出最小周长,若不存在,请说明理由。
(1)AC=8cm BC=6cm (2)y= (3)见解析 (4)16
(3)见解析 (4)16
【解析】
试题分析:(1)设AC=4x,BC=3x,根据勾股定理进行求解;(2)分两种情况来进行讨论,分别求出函数解析式;(3)利用三角形相似的条件来进行计算;(4)利用轴对称的性质来进行计算.

试题解析:(1)设AC=4x,BC=3x,在Rt△ABC中,AC²+BC²=AB²,即:(4x)²+(3x)²=10²,
解得:x=2,∴AC=8cm,BC=6cm;
(2)①、∵△QHB∽△ACB, ∴ ,
,
∴QH= x,y=
x,y= BP·QH=
BP·QH= (10-x)·
(10-x)· x=-
x=- x²+8x(0<x≤3),
x²+8x(0<x≤3),
②当点Q在边CA上运动时,过点Q作QH′⊥AB于H′,∵AP=x,∴BP=10-x,AQ=14-2x,∵△AQH′∽△ABC, ∴ ,即:
,即: ,解得:QH′=
,解得:QH′= (14-x),
(14-x),
∴y= PB·QH′=
PB·QH′= (10-x)·
(10-x)· (14-x)=
(14-x)= x²-
x²- x+42(3<x<7);
x+42(3<x<7);
∴y与x的函数关系式为:y= ;
;

(3)∵AP=x,AQ=14-x, ∵PQ⊥AB,∴△APQ∽△ACB,∴ ,
,
即: ,解得:x=
,解得:x= ,PQ=
,PQ= ,∴PB=10-x=
,∴PB=10-x= ,∴
,∴ ,
,
∴当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC不相似;
(4)存在,理由:∵AQ=14-2x=14-10=4,AP=x=5,∵AC=8,AB=10,∴PQ是△ABC的中位线,
∴PQ∥AB,∴PQ⊥AC, ∴PQ是AC的垂直平分线,∴PC=AP=5,∴当点M与P重合时,△BCM的周长最小, ∴△BCM的周长为:MB+BC+MC=PB+BC+PC=5+6+5=16,
∴△BCM的周长最小值为16。


考点:三角形相似的应用、勾股定理、二次函数的实际应用


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:[同步]2014年北师大版八年级上 2.4估算练习卷(解析版) 题型:?????
(2014•东西湖区二模)下列各数中,最小的是( )
A.﹣2 B.0 C.﹣ D.3
D.3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省温州市五校联赛九年级实验B班1月联考数学试卷(解析版) 题型:选择题
在半径为2的圆中,弦AB的长为2,则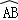 的长等于( )
的长等于( )
A.  B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期期中考试数学试卷(解析版) 题型:填空题
若关于x的一元二次方程kx2+4x+3=0有实根,则k的非负整数值是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期期中考试数学试卷(解析版) 题型:选择题
中国象棋红方棋子按兵种不同分布如下:1个帅、5个兵,“士、象、马、车、炮”各2个,将所有棋子反面朝上放在棋盘中,任取一个棋子,不是兵的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:解答题
(本题满分8分)已知抛物线y= +kx+b经过点P(2,-3),Q(-1,0).
+kx+b经过点P(2,-3),Q(-1,0).

(1)求抛物线的解析式.
(2)设抛物线顶点为 ,与
,与 轴交点为
轴交点为 .求
.求 的值.
的值.
(3)设抛物线与 轴的另一个交点为
轴的另一个交点为 ,求四边形
,求四边形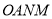 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:填空题
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1: ,点A的坐标为(0,1),则点E的坐标是 .
,点A的坐标为(0,1),则点E的坐标是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:解答题
如图,点A是x轴正半轴上的动点,点B的坐标为(0,4),将线段AB的中点绕点A按顺时针方向旋转90°得点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连接AC、BC、CD,设点A的横坐标为t.
(Ⅰ)线段AB与AC的数量关系是 ,位置关系是 .
(Ⅱ)当t=2时,求CF的长;
(Ⅲ)当t为何值时,点C落在线段BD上?求出此时点C的坐标;
(Ⅳ)设△BCE的面积为S,求S与t之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com