
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
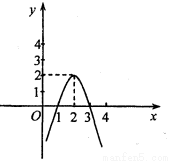
(1)写出y>0时,x的取值范围 ;
(2)写出y随x的增大而减小的自变量x的取值范围 ;
(3)求函数y=ax2+bx+c的表达式.
(1) 1<x<3;(2) x>2;(3) y=-2x2+8x-6.
【解析】
试题分析:(1)y>0是抛物线在x轴上方的部分,而抛物线与x轴交于(1,0),(3,0),结合图象,直接写出x的取值范围;
(2)抛物线的增减性是以对称轴分界的,根据对称轴及开口方向可确定此时自变量x的取值范围;
(3)可以通过已知抛物线与x轴的交点,设交点式;也可以设顶点式.
试题解析:(1)抛物线开口向下,与x轴交于(1,0),(3,0),
当y>0时,x的取值范围是:1<x<3;
(2)抛物线对称轴为直线x=2,开口向下,
y随x的增大而减小的自变量x的取值范围是x>2;
(3)抛物线与x轴交于(1,0),(3,0),
设解析式y=a(x-1)(x-3),把顶点(2,2)代入,
得2=a(2-1)(2-3),解得a=-2,
∴y=-2(x-1)(x-3),
即y=-2x2+8x-6.
考点:1.待定系数法求二次函数解析式;2.二次函数的图象.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:解答题
(本题满分8分)已知抛物线y= +kx+b经过点P(2,-3),Q(-1,0).
+kx+b经过点P(2,-3),Q(-1,0).

(1)求抛物线的解析式.
(2)设抛物线顶点为 ,与
,与 轴交点为
轴交点为 .求
.求 的值.
的值.
(3)设抛物线与 轴的另一个交点为
轴的另一个交点为 ,求四边形
,求四边形 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:选择题
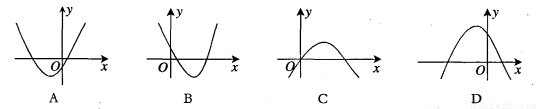
已知二次函数y=ax2+bx+c,若a<0,c>0,那么它的图象大致是( )
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:解答题
如图,点A是x轴正半轴上的动点,点B的坐标为(0,4),将线段AB的中点绕点A按顺时针方向旋转90°得点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连接AC、BC、CD,设点A的横坐标为t.
(Ⅰ)线段AB与AC的数量关系是 ,位置关系是 .
(Ⅱ)当t=2时,求CF的长;
(Ⅲ)当t为何值时,点C落在线段BD上?求出此时点C的坐标;
(Ⅳ)设△BCE的面积为S,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:选择题
已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=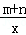 的图象可能是( )
的图象可能是( )
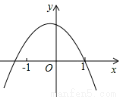
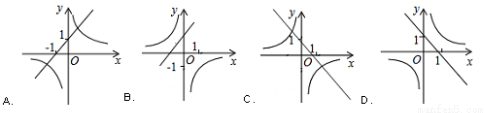
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:填空题
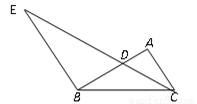
如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE//AC交CD的延长线于点E,且∠ACD=∠DBC,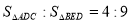 ,AB=10,则AC的长为
,AB=10,则AC的长为
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版) 题型:解答题
(本题满分8分)某公司欲招聘业务员一名,现对A、B、C三名候选人分别进行笔试、面试测试,成绩如下表:
测试项目 | 测试成绩(分) | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 85 | 90 |
面试 | 93 | 75 | 72 |
(1)如果按照三人测试成绩的平均成绩录取人选,那么谁将被录用?
(2)根据实际需要,公司想将丙录用,请兼顾笔试、面试两个方面,你确定的方案是什么?写出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com