练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，中，，．点是射线上一动点，过点作射线的垂线，垂足为点，点为的中点，连结，则的最小值为________．

    【答案】8

    【解析】

    取BC中点O，当点H、M、O在同一直线上时，线段HM的长有最小值，利用直角三角形的性质以及三角形中位线定理即可求解．

    在RtABC中，∠BAC=90，∠ABC=30，AB=16，

    ∴BC=2AC，

    ∵，即，

    解得：AC=16，BC=2AC =32，

    取BC中点O，如图：

    ∵OH是RtBCH斜边上的中线，

    ∴，

    ∵点O是BC的中点，点M为AB的中点，

    ∴OM=AC=8，OM∥AC，

    ∴OM⊥AB，

    当点H、M、O在同一直线上时，根据垂线段的性质，线段HM的长有最小值，

    ∴HM= OH- OM=16-8=8．

    故答案为：8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某工厂为了扩大生产，决定购买8台机器用于生产零件，现有甲、乙两种机器可供选择，其中甲型机器每日生产零件100个，乙型机器每日生产零件60个，经调查，购买3台甲型机器和2台乙型机器共需要31万元，购买一台甲型机器比购买一台乙型机器多2万元．

    (1)求甲、乙两种机器每台各多少万元？

    (2)如果工厂买机器的预算资金不超过46万元，那么该工厂有哪几种购买方案？

    (3)在(2)的条件下，如果要求该工厂购进的8台机器生产零件的日产量不低于550个，那么为了节约资金，应该选择哪种方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校准备租用一批汽车，现有甲、乙两种大客车，甲种客车每辆载客量45人，乙种客车每辆载客量30人，已知1辆甲种客车和3辆乙种客车共需租金1240元，3辆甲种客车和2辆乙种客车共需租金1760元．

    （1）求1辆甲种客车和1辆乙种客车的租金分别是多少元？

    （2）学校计划租用甲、乙两种客车共8辆，送330名师生集体外出活动，最节省的租车费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据新闻报道，作为宁波市政府民生实事之一的公共自行车建设工作已基本完成.某部门统计了今年4月份中的天的公共自行车日租车组情况，结果如图：

    （1）求这天日租车量的众数、中位数和平均数；

    （2）用（1）中的平均数估计4月份(天)共租车多少万车次？

    （3）2017年市政府在公共自行车建设项目中共投入万元，计划2019年投入万元，若这两年公共自行车建设投资的年增长率相同，求年增长率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．


    （1）求证：EB=GD且EB⊥GD；
    （2）若AB=2，AG=，求的长；

    （3）如图2，正方形AEFG绕点A逆时针旋转连结DE，BG，与的面积之差是否会发生变化？若不变，请求出与的面积之差；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知BE是△ABC的高，AE=BE，若要运用“HL”说明△AEF≌△BEC，还需添加条件：_________；若要运用“SAS”说明△AEF≌△BEC，还需添加条件：___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x、y的二元一次方程组x-y=3a①和x+3y=4-a②.

    （1）如果是方程①的解，求a的值;

    （2）当a=1时，求两个方程的公共解;

    （3）若方程组的解满足x≤0,求y的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，2×2网格（每个小正方形的边长为1）中，有A，O，B，C，D，E，F，H，G九个格点．抛物线l的解析式为y=x2+bx+c．

    （1）若l经过点O（0，0）和B（1，0），则b= ，c= ；它还经过的另一格点的坐标为 ．

    （2）若l经过点H（﹣1，1）和G（0，1），求它的解析式及顶点坐标；通过计算说明点D（1，2）是否在l上．

    （3）若l经过这九个格点中的三个，直接写出所有满足这样的抛物线的条数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：点、、不在同一条直线上，.

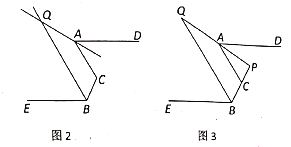
    （1）如图1，当，时，求的度数；

    （2）如图2，、分别为、的平分线所在直线，试探究与的数量关系；

    （3）如图3，在（2）的前提下，有，，直接写出的值.

    查看答案和解析>>

    同步练习册答案