
【题目】如图,已知BE是△ABC的高,AE=BE,若要运用“HL”说明△AEF≌△BEC,还需添加条件:_________;若要运用“SAS”说明△AEF≌△BEC,还需添加条件:___________.

科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,0)、B(3,0)、C(3,2)
(1)求证:BC⊥x轴;
(2)求△ABC的面积;
(3)若在y轴上有一点P,使S△ABP=2S△ABC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
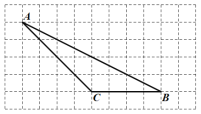
【题目】如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.

(1)求直线AC的解析式.
(2)在y轴上是否存在点P,直线PD与矩形对角线AC交于点M,使得△DMC为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)抛物线y=﹣x2经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且△ODE沿DE折叠后点O落在边AB上O′处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC和△DEF(它们均为锐角三角形)中,AC=DF,AB=DE.
(1)用尺规在图中分别作出AB、DE边上的高CG、FH(不要写作法,保留作图痕迹).
(2)如果CG=FH,猜测△ABC和△DEF是否全等,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB∥CD,E在直线AB上,且EF⊥EG,EF交直线CD于点M.EG交直线CD于点N.

(1)若∠1=34°,求∠2的度数;(2)若∠2=2∠1,直接写出图中等于4∠1的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县近两个多月持续高温而且没有降雨导致居民用水严重紧缺,为了加强市民的节水意识,我县制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨2元,超过10吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤10,请写出y与x的函数关系式.
(2)若x>10,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费29元,那么这个月该户用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com