
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA��y����������ϣ�OC��x����������ϣ�OA=1��OC=2����D�ڱ�OC����OD=1.25��

��1����ֱ��AC�Ľ���ʽ��
��2����y�����Ƿ���ڵ�P��ֱ��PD����ζԽ���AC���ڵ�M��ʹ����DMCΪ���������Σ������ڣ�ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3��������y=��x2��������ƽ�ƣ�����ʹ��ƽ�ƺ�������߹���D�͵�E����E��y���������ϣ�������ODE��DE�۵����O���ڱ�AB��O������
���𰸡���1��![]() ����2��P������Ϊ��0��
����2��P��������0�� ![]() ����0����
����0����![]() ����0��
����0�� ![]() ����0��
����0�� ![]() ���� ��3��������y=��x2������
���� ��3��������y=��x2������![]() ��λ��������ƽ��
��λ��������ƽ��![]() ��λ������ʹ��ƽ�ƺ�������߹���D�͵�E��
��λ������ʹ��ƽ�ƺ�������߹���D�͵�E��
�������������������1����ȷ��![]() ���
���![]() �����꣬Ȼ�����ô���ϵ������ֱ��
�����꣬Ȼ�����ô���ϵ������ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ���ۣ���
���ۣ���![]() ʱ��
ʱ�� ![]() �ⷽ�����
�ⷽ�����![]() �������
�������![]() �Ľ���ʽ���Ӷ��õ�
�Ľ���ʽ���Ӷ��õ�![]() �����ꣻ��
�����ꣻ��![]() ʱ����
ʱ����![]() ������꣬�������
������꣬�������![]() �Ľ���ʽ���Ӷ��õ�
�Ľ���ʽ���Ӷ��õ�![]() �����ꣻ��CM=CDʱ,
�����ꣻ��CM=CDʱ, ![]() �ⷽ�����
�ⷽ�����![]() ����ȷ��
����ȷ��![]() �Ľ���ʽ���Ӷ��õ�
�Ľ���ʽ���Ӷ��õ�![]() �����ꣻ
�����ꣻ
��3����ͼ2����O��H��x����H,��![]() ��O��(m,1)�����ù��ɶ����õ�
��O��(m,1)�����ù��ɶ����õ�![]() ,���
,���![]() ��m=2ʱ�����
��m=2ʱ�����![]() ���õ�
���õ�![]() ���ô���ϵ������������߽���ʽΪ
���ô���ϵ������������߽���ʽΪ![]() Ȼ�����������ߵ�ƽ�Ʊ任��⣻��
Ȼ�����������ߵ�ƽ�Ʊ任��⣻��![]() ʱ��ͬ���ɵ������߽���ʽΪ
ʱ��ͬ���ɵ������߽���ʽΪ![]() �����������ߵ�ƽ�Ʊ任��⣮
�����������ߵ�ƽ�Ʊ任��⣮
���������(1)��OA=1,OC=2,
��A(0,1),C(2,0)��
��ֱ��AC�Ľ���ʽΪy=kx+b��
��A(0,1),C(2,0)�����![]() ���
���
��ֱ��AC�Ľ���ʽΪ![]()
(2)����.

![]()
��![]()
��DM=DCʱ, ![]() ���
���![]() (��ȥ),��
(��ȥ),��![]() ,��ʱMD�Ľ���ʽΪ
,��ʱMD�Ľ���ʽΪ![]() P������Ϊ
P������Ϊ![]()
��MD=MCʱ,��M�������Ϊ![]() ��ʱMD�Ľ���ʽΪ
��ʱMD�Ľ���ʽΪ![]() P������Ϊ
P������Ϊ![]()
��CM=CDʱ, ![]() ���
���![]()
�� ��
��
��ʱMD�Ľ���ʽΪ ��
�� P������Ϊ
P������Ϊ ��
��
��������,P������Ϊ![]() ��
��![]() ��
�� ��
�� ;
;
(3)��ODE��DE�۵����O���ڱ�AB��O����,��ͼ2,��O��H��x����H,��![]()
��O��(m,1)��
��![]() ��,
��, ![]() , ���
, ���![]()
��m=2ʱ,AO��=2,��EO��=EO=EA+1��
![]() ,���
,���![]()
![]()
��ƽ�Ƶ������߽���ʽΪ![]()
��![]() �����
����� ���
���
�������߽���ʽΪ![]()
![]()
��������![]() ������
������![]() ��λ,������ƽ��
��λ,������ƽ��![]() ��λ������ʹ��ƽ�ƺ�������߹���D�͵�E��
��λ������ʹ��ƽ�ƺ�������߹���D�͵�E��
��![]() ʱ,
ʱ, ![]() ,��EO��=EO=1AE��
,��EO��=EO=1AE��
![]() ���
���![]()
![]()
ͬ���ɵ������߽���ʽΪ![]()
![]()
��������![]() ������
������![]() ��λ,������ƽ��
��λ,������ƽ��![]() ��λ������ʹ��ƽ�ƺ�������߹���D�͵�E.
��λ������ʹ��ƽ�ƺ�������߹���D�͵�E.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���꼶ѧ�������������ѧУ��֯��һ�����ܲ��ԣ������ѡȡ50��ѧ���ijɼ�����ͳ�ƣ��ó����ͳ�Ʊ���ͳ��ͼ(���в������ݲ�����ʧ��������ĸm��n��ʾ).
�ɼ��ȼ� | ���� | ���� | �ϸ� | ���ϸ� |
���� | m | 30 | n | 5 |
�����ͼ�����ṩ����Ϣ�ش��������⣺
(1)ͳ�Ʊ��е�m�� ��n�� ������ȫƵ���ֲ�ֱ��ͼ��
(2)����У���꼶��500��ѧ������ݴ˹��Ƹ�У���꼶ѧ���������ü��������ϵ�ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
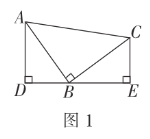
����Ŀ����1����ͼ1����![]() �У�
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ������
������![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����֤��
����֤��![]() ��
��
��2����ͼ2����֪��![]() ����
����![]() ��
��![]() ��
��![]() ���ҵ�
���ҵ�![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���![]() ����ֱ�ߵı���ʽ��
����ֱ�ߵı���ʽ��
��3����ͼ3���ڳ�����![]() �У�
�У�![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ������Ϊ
������Ϊ![]() ����
����![]() �ֱ����������ϣ���
�ֱ����������ϣ���![]() ���߶�
���߶�![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ��ֱ��
��ֱ��![]() �ϵĶ�������
�ϵĶ�������![]() ����Ҳ࣮��
����Ҳ࣮��![]() ���Ե�
���Ե�![]() Ϊֱ�Ƕ���ĵ���ֱ�������Σ��������
Ϊֱ�Ƕ���ĵ���ֱ�������Σ��������![]() �����꣮
�����꣮


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
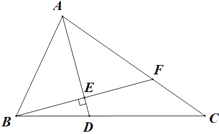
����Ŀ����ͼ���ڡ�ABC�У���ABC=65������C=35����AD�ǡ�ABC�Ľ�ƽ����.
(1)���ADC�Ķ���.
(2)����B��BE��AD�ڵ�E��BE�ӳ��߽�AC�ڵ�F.���AFE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ű�������Ϊ��������������ʵ��֮һ�Ĺ������г����蹤���ѻ������.ij����ͳ���˽���4�·��е�![]() ��Ĺ������г����������������ͼ��
��Ĺ������г����������������ͼ��

��1������![]() �����������������λ����ƽ������
�����������������λ����ƽ������
��2���ã�1���е�ƽ��������4�·�(![]() ��)��������Σ�
��)���������
��3��2017���������ڹ������г�������Ŀ�й�Ͷ��![]() ��Ԫ���ƻ�2019��Ͷ��
��Ԫ���ƻ�2019��Ͷ��![]() ��Ԫ���������깫�����г�����Ͷ�ʵ�����������ͬ�����������ʣ�
��Ԫ���������깫�����г�����Ͷ�ʵ�����������ͬ�����������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��![]() ��y1����B��2��y2��Ϊ����������y=
��y1����B��2��y2��Ϊ����������y=![]() ͼ���ϵ����㣬����P��x��0����x�����������˶������߶�AP���߶�BP֮��ﵽ���ʱ����P��������_____��
ͼ���ϵ����㣬����P��x��0����x�����������˶������߶�AP���߶�BP֮��ﵽ���ʱ����P��������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BE����ABC�ĸߣ�AE=BE����Ҫ������HL��˵����AEF�ա�BEC����������������_________����Ҫ������SAS��˵����AEF�ա�BEC����������������___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1������ABC��,��ACB��ֱ��,��ABC=60����AD��CE��BF�ֱ��ǡ�BAC����BCA����ABC��ƽ���ߣ�AD��CE��BF�ཻ�ڵ�F.
���������AFC�Ķ�����˵�����ɣ�
�������ж�FE��FD֮���������ϵ��˵�����ɡ�
��2����ͼ2,����ABC��,�����ACB����ֱ��,��(1)�е�������������,���ж��߶�AE��CD��AC֮���������ϵ��˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PΪƽ���ı���ABCD��AD��һ�㣬E��F�ֱ�ΪPB��PC���е㣬��PEF����PDC����PAB������ֱ�ΪS��S1��S2����S=2����S1+S2=�� ��

A. 4 B. 6 C. 8 D. ����ȷ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com