
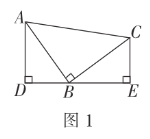
【题目】(1)如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证:![]() .
.
(2)如图2,已知点![]() ,点
,点![]() ,
,![]() ,
,![]() ,且点
,且点![]() 在第一象限,求
在第一象限,求![]() 所在直线的表达式.
所在直线的表达式.
(3)如图3,在长方形![]() 中,
中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在
上的动点且在![]() 轴的右侧.若
轴的右侧.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请求出点
为直角顶点的等腰直角三角形,请求出点![]() 的坐标.
的坐标.


【答案】(1)详见解析;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)通过∠BCE+∠EBC=90°,∠ABD+∠EBC=90°得∠ABD=∠BCE,再结合∠ADC=∠BEC=90°,CB=CA即可得证;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,由(1)可知
,由(1)可知![]() ,
,![]() ,则
,则![]() ,进而求得点C坐标,再结合点A坐标利用待定系数法求解即可;
,进而求得点C坐标,再结合点A坐标利用待定系数法求解即可;
(3)设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,由(1)得
,由(1)得![]() ,进而通过
,进而通过![]() 列出方程求解即可.
列出方程求解即可.
(1)证明:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
(2)解:如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
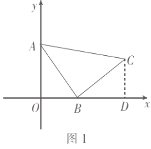
由(1)可知![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设![]() 所在直线的表达式为
所在直线的表达式为![]() ,
,
将![]() ,
,![]() 代入得
代入得![]() 解得
解得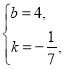
![]() 直线
直线![]() 在直线的表达式为
在直线的表达式为![]() .
.
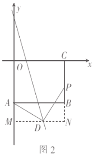
(3)解:∵点D在y=﹣3x+6上,
∴设点![]() 的坐标为
的坐标为![]() .
.
如图2,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
由题意可得![]() ,(AAS)
,(AAS)
![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用树状图或列表法求恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其余都相同的乒乓球,设计一个摸球的实验(至少摸两次),
并根据该实验写出一个发生概率与(1)所求概率相同的事件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,0)、B(3,0)、C(3,2)
(1)求证:BC⊥x轴;
(2)求△ABC的面积;
(3)若在y轴上有一点P,使S△ABP=2S△ABC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
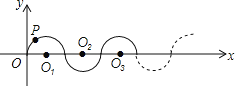
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…,组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是( )
个单位长度,则第2019秒时,点P的坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎解方程![]() 时出现了错误,其解答过程如下:
时出现了错误,其解答过程如下:
解:方程两边都乘以![]() ,得
,得![]() ,(第1步)
,(第1步)
移项,合并同类项,得![]() ,(第2步)
,(第2步)
经检验,![]() 是原方程的解.(第3步)
是原方程的解.(第3步)
(1)小马虎解答过程是从第______步开始出错的,出错的原因是___________;
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
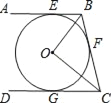
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
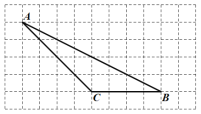
【题目】如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.

(1)求直线AC的解析式.
(2)在y轴上是否存在点P,直线PD与矩形对角线AC交于点M,使得△DMC为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)抛物线y=﹣x2经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且△ODE沿DE折叠后点O落在边AB上O′处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB∥CD,E在直线AB上,且EF⊥EG,EF交直线CD于点M.EG交直线CD于点N.

(1)若∠1=34°,求∠2的度数;(2)若∠2=2∠1,直接写出图中等于4∠1的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com