
【题目】如图,已知:AB∥CD,E在直线AB上,且EF⊥EG,EF交直线CD于点M.EG交直线CD于点N.

(1)若∠1=34°,求∠2的度数;(2)若∠2=2∠1,直接写出图中等于4∠1的角.
【答案】(1)∠2=56°;(2)等于4∠1的角为∠FMN,∠CME,∠MEB
【解析】
(1)依据AB∥CD,可得∠1=∠GEB=34°,依据EF⊥EG,即可得到∠2=180°-90°-34°=56°;
(2)依据∠2=2∠1,∠1=∠GEB,即可得到∠GEB=30°=∠1,进而得出∠FMN=∠CME=∠MEB=120°,即可得到图中等于4∠1的角为∠FMN,∠CME,∠MEB.
(1)∵AB∥CD,
∴∠1=∠GEB=34°,
∵EF⊥EG,
∴∠2=180°﹣90°﹣34°=56°;
(2)∵∠2=2∠1,∠1=∠GEB,
∴∠2=2∠GEB,
又∵∠2+∠GEB=90°,
∴∠GEB=30°=∠1,
∴4∠1=120°,∠2=60°,
∴∠FMN=∠CME=∠MEB=120°,
即图中等于4∠1的角为∠FMN,∠CME,∠MEB.


科目:初中数学 来源: 题型:
【题目】(1)如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证:![]() .
.
(2)如图2,已知点![]() ,点
,点![]() ,
,![]() ,
,![]() ,且点
,且点![]() 在第一象限,求
在第一象限,求![]() 所在直线的表达式.
所在直线的表达式.
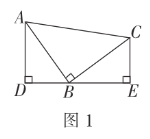
(3)如图3,在长方形![]() 中,
中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在
上的动点且在![]() 轴的右侧.若
轴的右侧.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请求出点
为直角顶点的等腰直角三角形,请求出点![]() 的坐标.
的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BE是△ABC的高,AE=BE,若要运用“HL”说明△AEF≌△BEC,还需添加条件:_________;若要运用“SAS”说明△AEF≌△BEC,还需添加条件:___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠ACB是直角,∠ABC=60°,AD、CE、BF分别是∠BAC、∠BCA、∠ABC的平分线,AD、CE、BF相交于点F.
①请求出∠AFC的度数并说明理由;
②请你判断FE与FD之间的数量关系并说明理由。
(2)如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请判断线段AE、CD、AC之间的数量关系并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中,有A,O,B,C,D,E,F,H,G九个格点.抛物线l的解析式为y=![]() x2+bx+c.
x2+bx+c.
(1)若l经过点O(0,0)和B(1,0),则b= ,c= ;它还经过的另一格点的坐标为 .
(2)若l经过点H(﹣1,1)和G(0,1),求它的解析式及顶点坐标;通过计算说明点D(1,2)是否在l上.
(3)若l经过这九个格点中的三个,直接写出所有满足这样的抛物线的条数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形平移与旋转”为主题开展数学活动,![]() 和
和![]() 是两个等边三角形纸片,其中,
是两个等边三角形纸片,其中,![]() .
.
解决问题
(1)勤奋小组将![]() 和
和![]() 按图1所示的方式摆放(点
按图1所示的方式摆放(点![]() 在同一条直线上) ,连接
在同一条直线上) ,连接![]() .发现
.发现![]() ,请你给予证明;
,请你给予证明;

(2)如图2,创新小组在勤奋小组的基础上继续探究,将![]() 绕着点
绕着点![]() 逆时针方向旋转,当点
逆时针方向旋转,当点![]() 恰好落在
恰好落在![]() 边上时,求
边上时,求![]() 的面积;
的面积;

拓展延伸
(3)如图3,缜密小组在创新小组的基础上,提出一个问题: “将![]() 沿
沿![]() 方向平移
方向平移![]() 得到
得到![]() 连接
连接![]() ,当
,当![]() 恰好是以
恰好是以![]() 为斜边的直角三角形时,求
为斜边的直角三角形时,求![]() 的值.请你直接写出
的值.请你直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数![]() 的图象与性质.
的图象与性质.
因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
| … |
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
| … |
|
| 1 | 2 | 4 |
|
| 1 |
|
| … |
| … |
|
| 2 | 3 | 5 |
|
| 0 |
|
| … |
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出了相应的点(如图所示).
相应的函数值为纵坐标,描出了相应的点(如图所示).
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而 ;(填“增大”或“减小”)
的增大而 ;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③![]() 图象关于点 成中心对称.(填点的坐标)
图象关于点 成中心对称.(填点的坐标)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受台风影响的区域.
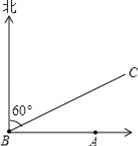
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com