
����Ŀ��Ŀǰ���ܵ��ڸ������ѻ����ռ�������ij�������ؼ���ũ������ƹ㣬Ϊ��Ӧ���٣����������̳�����![]() Ԫ�������ͺ��������ֽ��ܵƣ��������ͺŽ��ܵƵĽ��ۡ��ۼ����:
Ԫ�������ͺ��������ֽ��ܵƣ��������ͺŽ��ܵƵĽ��ۡ��ۼ����:
���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� | |
���� |
|
|
���� |
|
|
�ر�˵����ë����=�ۼ�-���ۣ�
��1�����������̳����ۼ��ͽ��ܵ�һֻë������______Ԫ��
��2��������������̳�����ף������ֽ��ܵƹ�![]() ֻ���������˼��ͽ��ܵƶ���ֻ?
ֻ���������˼��ͽ��ܵƶ���ֻ?
��3�����ڳ��������̳��������ͽ��ܵ�![]() ֻ����������̳�����һ����������ܵ�ʱ�����ë�����Ƕ���?
ֻ����������̳�����һ����������ܵ�ʱ�����ë�����Ƕ���?
���𰸡�(1)5;(2) ���˼��ͽ��ܵ�15ֻ;(3)1080Ԫ.
��������
(1)�������й�ʽ��ʽ���㼴��.
(2)�����˼��ͽ��ܵ�xֻ,�����ͽ��ܵ�100-xֻ,����������4200�г����̽������.
(3)��������ͽ��ܵƵ�����,�ٽ����������ܵƵ�ë������Ӽ������.
(1)�����������̳����ۼ��ͽ��ܵ�һֻë������30��25=5Ԫ.
(2)�����˼��ͽ��ܵ�xֻ,���������:
25x+45(100��x)=4200,
���x=15,
��:���˼��ͽ��ܵ�15ֻ.
(3)���ͽ��ܵƵ�����:(4200��96��25)��45=40ֻ.
����ë����:96��(30-25)+40��(60-45)=480+600=1080Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90����AC=BC=4��D��AB���е㣬��E��F�ֱ���AC��BC�����˶�����E�����A��C�غϣ����ұ���AE=CF������DE��DF��EF���ڴ��˶��仯�Ĺ����У������н��ۣ�
�١�DFE�ǵ���ֱ�������Σ�
���ı���CEDF������Ϊ�����Σ�
���ı���CEDF��������Eλ�õĸı�������仯��
����C���߶�EF��������Ϊ![]() ��
��
������ȷ���۵ĸ����ǣ� ��

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͼ�α仯�Ĺ��ɣ�ͼ�е�ʡ�Ժ����ɫ�����εĸ��������ǣ� ��


![]()

A.2016B.2017C.2018D.2019
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F�ֱ�Ϊ����ABCD�ı�AD��BC�ϵĵ㣬AE=CF����֤��BE=DF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3��3�ķ����У�ÿ�С�ÿ�м��Խ����ϵ�3������ʽ�ĺͶ���ȣ����ǰ������ķ���ͼ�������Ⱥ�������ͼ�����Ⱥ����У�ÿ�С�ÿ�м��Խ����ϵ�3������ʽ�ĺͶ�����15.
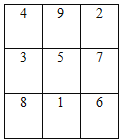
��1��ͼ1����ʾ���ִ���ʽ�����Ⱥ������ɵ�a=_______����b�Ĵ���ʽ��ʾ����
��2��ͼ2����ʾ���ִ���ʽ�����Ⱥ������ɵ�a=__________,b=__________;
��3��ͼ3����ʾ���ִ���ʽ�����Ⱥ�������b��ֵ����д�����������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��b��c���dz�������ͼ���㣨1��0���ͣ�0��2����
��1������2��x��2ʱ����y��ȡֵ��Χ��
��2����֪��P��m��n���ڸú�����ͼ���ϣ���m+n=1�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
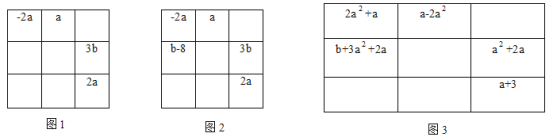
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF.����DE������E��EG��DE��ʹEG=DE������FG��FC
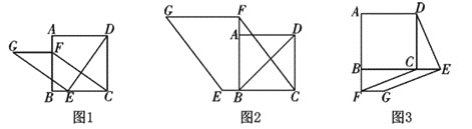
��1�����ж�:FG��CE��������ϵ�� ________��λ�ù�ϵ��________��
��2����ͼ2������E��F�ֱ��DZ�CB��BA�ӳ����ϵĵ㣬�����������䣬(1)�н����Ƿ���Ȼ����?�������жϲ�����֤��;
��3����ͼ3������E��F�ֱ��DZ�BC��AB�ӳ����ϵĵ㣬�����������䣬(1)�н����Ƿ���Ȼ����?��ֱ��д������жϡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʮһ���ƽ����ڼ䣬������Ůɽ�羰��7�������ÿ�����ε������仯���±���������ʾ��ǰһ����������������ʾ��ǰһ���ٵ���������
���� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯 ��λ������ | +1.2 | +0.4 | +0.8 | ��0.4 | ��0.8 | +0.2 | ��1.2 |
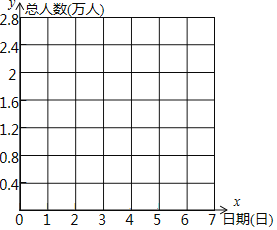
��1����9��30�յ��ο�������Ϊa�����ú�a��ʽ�ӱ�ʾ10��5�յ��ο��������� �����ˣ�
��2���ж��������ο������������� ���գ����ٵ����� ���գ�
��3����9��30�յ��ο�����Ϊ0�㣬������ͳ��ͼ��ʾ��7����ο���������������仯�����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC��AB��AC��24���ף���B����C��BC��16���ף���DΪAB���е㣮��P���߶�BC����4����/����ٶ���B����C���˶���ͬʱ����Q���߶�CA����C����A���˶�������Q���˶��ٶ�Ϊv����/�룬����BPD����CQPȫ��ʱ��v��ֵΪ_____ ����/�룮
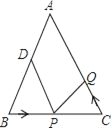
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com