
����Ŀ����ͼ������ABC�У���C=90����AC=BC=4��D��AB���е㣬��E��F�ֱ���AC��BC�����˶�����E�����A��C�غϣ����ұ���AE=CF������DE��DF��EF���ڴ��˶��仯�Ĺ����У������н��ۣ�
�١�DFE�ǵ���ֱ�������Σ�
���ı���CEDF������Ϊ�����Σ�
���ı���CEDF��������Eλ�õĸı�������仯��
����C���߶�EF��������Ϊ![]() ��
��
������ȷ���۵ĸ����ǣ� ��

A.1��B.2��C.3��D.4��
���𰸡�B
��������
������CD����ͼ1����
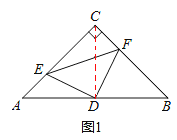
�ߡ�ABC�ǵ���ֱ�������Σ����DCB=��A=45����CD=AD=DB��
��AE=CF�����ADE�ա�CDF��SAS����
��ED=DF����CDF=��EDA��
�ߡ�ADE+��EDC=90�������EDC+��CDF=��EDF=90����
���DFE�ǵ���ֱ�������Ρ�
�ʴ˽�����ȷ��
����E��F�ֱ�ΪAC��BC�е�ʱ��������������λ�߶�����DEƽ���ҵ���![]() BC��
BC��
���ı���CEDF��ƽ���ı��Ρ�
����E��F�ֱ�ΪAC��BC�е㣬AC=BC�����ı���CEDF�����Ρ�
���ߡ�C=90�������ı���CEDF�������Ρ�
�ʴ˽��۴���
����ͼ2���ֱ����D����DM��AC��DN��BC���ڵ�M��N��
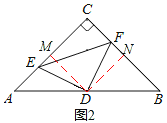
������֪�ı���CMDN�������Σ���DM=DN��
������֪��DFE�ǵ���ֱ�������Σ���DE=DF��
��Rt��ADE��Rt��CDF��HL����
���ɸ����֪�ı���CEDF���������������CMDN�����
���ı���CEDF����������Eλ�õĸı�������仯��
�ʴ˽��۴���
����������DEF�ǵ���ֱ�������Σ���FE=![]() DF��
DF��
��DF��BC��ֱ����DF��Сʱ�� EFȡ��Сֵ2![]() ����ʱ��C���߶�EF��������Ϊ
����ʱ��C���߶�EF��������Ϊ![]() ��
��
�ʴ˽�����ȷ��
����ȷ����2�����٢�����ѡB��
���ڴ�������⣡



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
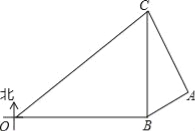
����Ŀ����ij�κ��Ͼ���ѧϰ�ڼ䣬�Ҿ�Ϊȷ����OBC�����ڵİ�ȫ������Dz���Ҿ����ֱ���O��B��C�������OBC�������״���ʾͼ�ϣ�����B�ھ���O����������80���ﴦ������C�ھ���B����������60���ﴦ�����Ҿ�����װ������ͬ��̽���״�״����Ч̽�ⷶΧ�ǰ뾶Ϊr��Բ������ֻ�����ں�ƽ���ϵ�̽�⣩
��1�������Ҿ���Ҫ����OBC���������ä���أ����״����Ч̽��뾶r����Ϊ���ٺ��
��2������һ�ҵн�A�Ӷ����ӽ���OBC������ijһʱ�̾���B���Aλ�ڱ�ƫ��60�������ϣ�ͬʱ����C���Aλ����ƫ��30�������ϣ����ʱ�н�A����OBC�������̾���Ϊ���ٺ��
��3�����н�A����̾����·����20![]() ����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
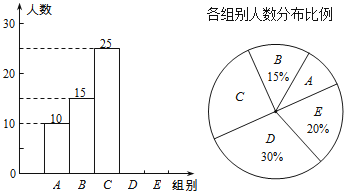
����Ŀ��ijУ����ȫ��ѧ����������д��������ÿλѧ����д����39��![]() �����ȡ�˲���ѧ������д��������Ƴ����µ�ͼ����
�����ȡ�˲���ѧ������д��������Ƴ����µ�ͼ����
��� | ��ȷ����x | ���� |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
����������Ϣ����������⣺
![]() ͳ�Ʊ��е�
ͳ�Ʊ��е�![]() ______��
______��![]() ______������ȫ����ͳ��ͼ��
______������ȫ����ͳ��ͼ��
![]() ����ͳ��ͼ����C��������Ӧ��Բ�ĽǵĶ�����______��
����ͳ��ͼ����C��������Ӧ��Բ�ĽǵĶ�����______��
![]() ��֪��У����900��ѧ���������д��ȷ���ֵĸ�������24����Ϊ���ϸ�������Ƹ�У������д�������ϸ��ѧ��������
��֪��У����900��ѧ���������д��ȷ���ֵĸ�������24����Ϊ���ϸ�������Ƹ�У������д�������ϸ��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н�������ȷ���ǣ�������
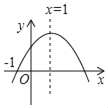
A. a��0 B. c��0 C. ����1��x��3ʱ��y��0 D. ��x��1ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������������ȱˮ�Ĺ���֮һ��Ϊ�˳�������Լ��ˮ������������С���������ڰ��50��ͬѧ�У����������10��ͬѧ��ͥ��һ����¾���ˮ������λ��t����������������������µ�����ͳ��ͼ
��1������10���������ݵ�ƽ��������������λ����
��2�������������ݣ�����С�����ڰ�50��ͬѧ��ͥ���¾���ˮ��������7 t��Լ�ж��ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�����ڱ�Уѧ���п�չ����������ë��ƹ�������ֻ��Ϊ���˽�ѧ���������ֻ��ϲ�������ѧУ��������˸�Уm��ѧ����������ϲ����һ�ֻ��ÿ��ѧ����ѡһ����ֻ�ܴ������ֻ��ѡ��һ�֣����ֽ�����Ľ�����Ƴ����²�������ͳ��ͼ���������ͼ�е���Ϣ������������⣮
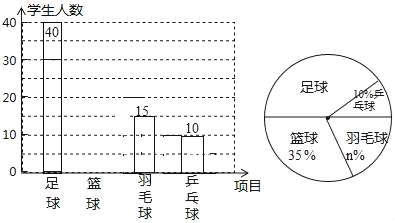
��1��m=�� ����n=�� ����
��2���벹ȫͼ�е�����ͼ��
��3������ͳ��ͼ�У����ֵ�Բ�Ľ����� ���ȣ�
��4�����ݳ�������Ľ���������ȫУ1800��ѧ���У���Լ�ж�����ϲ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������OABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����B������Ϊ��3��4������D������Ϊ��2��0����EΪAB�ϵĵ㣬����CDE���ܳ���Сʱ����E������Ϊ��������
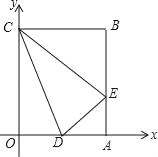
A. ��1��3�� B. ��3��1�� C. ��4��1�� D. ��3��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨѶ������Ѹ�ͷ�չ��������֮��Ĺ�ͨ��ʽ����������ݣ�ijУ��ѧ��ȤС������ˡ�����ϲ���Ĺ�ͨ��ʽ�������ʾ���ÿ�˱�ѡ��ֻѡһ�֣�����ȫУ��Χ����������˲���ѧ������ͳ�ƽ������������������������ͳ��ͼ������ͼ����������Ϣ����������⣺

��1�����ͳ�ƹ������ ����ѧ����������ͳ��ͼ�У���ʾ��QQ��������Բ�ĽǵĶ���Ϊ �� ��
��2��������ͳ��ͼ����������
��3����У����1500��ѧ��������Ƹ�У��ϲ���á��š����й�ͨ��ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ܵ��ڸ������ѻ����ռ�������ij�������ؼ���ũ������ƹ㣬Ϊ��Ӧ���٣����������̳�����![]() Ԫ�������ͺ��������ֽ��ܵƣ��������ͺŽ��ܵƵĽ��ۡ��ۼ����:
Ԫ�������ͺ��������ֽ��ܵƣ��������ͺŽ��ܵƵĽ��ۡ��ۼ����:
���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� | |
���� |
|
|
���� |
|
|
�ر�˵����ë����=�ۼ�-���ۣ�
��1�����������̳����ۼ��ͽ��ܵ�һֻë������______Ԫ��
��2��������������̳�����ף������ֽ��ܵƹ�![]() ֻ���������˼��ͽ��ܵƶ���ֻ?
ֻ���������˼��ͽ��ܵƶ���ֻ?
��3�����ڳ��������̳��������ͽ��ܵ�![]() ֻ����������̳�����һ����������ܵ�ʱ�����ë�����Ƕ���?
ֻ����������̳�����һ����������ܵ�ʱ�����ë�����Ƕ���?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com