
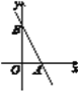
【题目】如图,已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
(1)点A的坐标为________,点B的坐标为________.
(2)求△AOB的面积.
(3)直线AB上是否存在一点C(点C与点B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
【答案】(1) (3,0),(0,6);(2)9;(3)存在,点C的坐标为(6,-6).
【解析】
(1)根据坐标轴上点的坐标特征求![]() 点和
点和![]() 点坐标;
点坐标;
(2)根据三角形面积公式求解;
(3)根据一次函数图象上点的坐标特征,设![]() ,则利用三角形面积公式得到
,则利用三角形面积公式得到![]() ,然后解绝对值方程求出
,然后解绝对值方程求出![]() 的值即可得到
的值即可得到![]() 点坐标.
点坐标.
(1)当y=0时,-2x+6=0,解得x=3,则A点的坐标为(3,0);当x=0时,y=-2x+6=6,则B点的坐标为(0,6).
(2)S△AOB=![]() ×3×6=9.
×3×6=9.
(3)存在.理由如下:设点C的坐标为(t,-2t+6).
因为△AOC的面积等于△AOB的面积,所以![]() ×3×|-2t+6|=9,解得t1=6,t2=0(与点B重合,舍去).所以点C的坐标为(6,-6).
×3×|-2t+6|=9,解得t1=6,t2=0(与点B重合,舍去).所以点C的坐标为(6,-6).


科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与直线y= ![]() x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3, ![]() ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.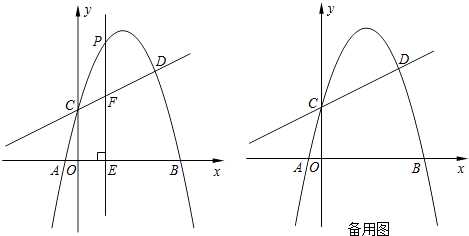
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.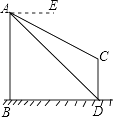
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
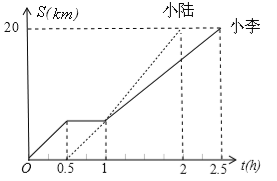
【题目】小李和小陆从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示,根据图中的信息,有下列说法:
(1)他们都行驶了20 km;
(2)小陆全程共用了1.5h;
(3)小李和小陆相遇后,小李的速度小于小陆的速度
(4)小李在途中停留了0.5h。
其中正确的有
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数a、b、c满足a+b=ab=c,有下列结论:
①若c≠0,则![]() ;②若a=3,则b+c=9;
;②若a=3,则b+c=9;
③若a=b=c,则abc=0;④若a、b、c中只有两个数相等,则a+b+c=8.
其中正确的是 (把所有正确结论的序号都选上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).

(1)写出△ABC的面积:_______.
(2)画出△ABC关于y轴对称的△A1B1C1.
(3)写出点B及其对称点B1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com