
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.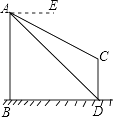
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
【答案】
(1)
解:根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)
解:延长AE、DC交于点F,根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
∴CF=AFtan∠FAC=60× ![]() =20
=20 ![]() ,
,
又∵FD=60,
∴CD=60﹣20 ![]() ,
,
∴建筑物CD的高度为(60﹣20 ![]() )米.
)米.
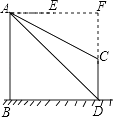
【解析】(1)根据题意得:BD∥AE,从而得到∠BAD=∠ADB=45°,利用BD=AB=60,求得两建筑物底部之间水平距离BD的长度为60米;(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,根据AF=BD=DF=60,在Rt△AFC中利用∠FAC=30°求得CF,然后即可求得CD的长.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③等角的邻补角相等;④垂直于同一条直线的两条直线互相平行.其中真命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度![]() (厘米)与燃烧时间
(厘米)与燃烧时间![]() (小时)之间的关系如图所示,其中乙蜡烛燃烧时
(小时)之间的关系如图所示,其中乙蜡烛燃烧时![]() 与
与![]() 之间的函数关系式是
之间的函数关系式是![]() .
.
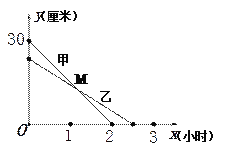
(1)甲蜡烛燃烧前的高度是_________厘米,乙蜡烛燃烧的时间是________小时.
(2)求甲蜡烛燃烧时![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)求出图中交点![]() 的坐标,并说明点
的坐标,并说明点![]() 的实际意义.
的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
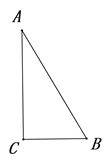
已知:如图,在![]() △
△![]() 中,
中, ![]() °,
°,![]() °.
°.
求证: ![]() .
.
证明:
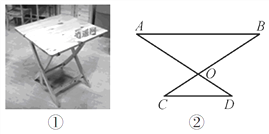
【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得![]() ,
, ![]() ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度![]() .
.
求:桌面与地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面上有n条直线,其中没有两条直线互相平行(即每两条直线都相交),也没有三条或三条以上的直线通过同一点.试求:
(1)这n条直线共有多少个交点?
(2)这n条直线把平面分割为多少块区域?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=![]() ,b=
,b=![]() ,c=
,c=![]() ; ②a=6,b=8,c=10; ③a=7,b=24,c=25;
; ②a=6,b=8,c=10; ③a=7,b=24,c=25;
④a=2,b=3,c=4.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.
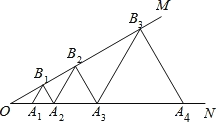
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com