Question

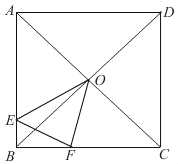
【题目】如图，O为正方形ABCD对角线的交点，E为AB边上一点，F为BC边上一点，△EBF的周长等于BC的长．

（1）若AB=12，BE=3，求EF的长；

（2）求∠EOF的度数；

（3）若OE=OF，求的值．

Answer 1

【答案】（1）EF =5；（2）∠EOF=45°；（3）．

【解析】

（1）设BF=x，则FC=BC﹣BF=12﹣x，根据BE=3，且BE+BF+EF=BC，表示出

EF，在Rt△BEF中，根据勾股定理即可求出，即可求出EF的长；

（2）如图，在FC上截取FM=FE，连接OM，分别证明△OBE≌△OCM，△OFE≌△OFM，根据全等三角形的性质即可求出∠EOF的度数；

（3）证明△AOE∽△CFO．根据相似三角形的性质得到

即可求出的值．

（1）设BF=x，则FC=BC﹣BF=12﹣x，

∵BE=3，且BE+BF+EF=BC，

∴EF=9﹣x，

在Rt△BEF中，由BE2+BF2=EF2可得32+x2=（9﹣x）2，

解得：x=4，

则EF=9﹣x=5；

（2）如图，在FC上截取FM=FE，连接OM，

∵C△EBF的周长=BE+EF+BF=BC，则BE+EF+BF=BF+FM+MC，

∴BE=MC，

∵O为正方形中心，

∴OB=OC，∠OBE=∠OCM=45°，

在△OBE和△OCM中，

∵

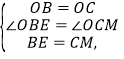
∴△OBE≌△OCM，

∴∠EOB=∠MOC，OE=OM，

∴∠EOB+∠BOM=∠MOC+∠BOM，即∠EOM=∠BOC=90°，

在△OFE与△OFM中，

∵

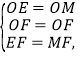
∴△OFE≌△OFM（SSS），

∴

（3）证明：由（2）可知：∠EOF=45°，

∴∠AOE+∠FOC=135°，

∵∠EAO=45°，

∴∠AOE+∠AEO=135°，

∴∠FOC=∠AEO，

∵∠EAO=∠OCF=45°，

∴△AOE∽△CFO．

∴

∴

∵AO=CO，

∴

∴