
����Ŀ����ͬһƽ���ڣ���һ���㵽һ��ֱ�ߵľ��벻����1�����������Ǹ�ֱ�ߵ������µ�����
��ƽ��ֱ������ϵ�У���֪��M��1��0��������M��ֱ��lƽ����y�ᣬ��A����1��a������B��b��2a������ C����![]() ��a��1������������ABC����ƽ�ƣ�ƽ�ƺ��A�Ķ�Ӧ��ΪD����B�Ķ�Ӧ��ΪE����C�Ķ�Ӧ��ΪF��
��a��1������������ABC����ƽ�ƣ�ƽ�ƺ��A�Ķ�Ӧ��ΪD����B�Ķ�Ӧ��ΪE����C�Ķ�Ӧ��ΪF��
��1�����жϵ�A�Ƿ���ֱ��l�������µ�������˵�����ɣ�
��2������F�պ�����ֱ��l�ϣ�F��������Ϊa+b����E����x���ϣ���������MFD�����Ϊ![]() �����жϵ�B�Ƿ���ֱ��l�������µ�������˵�����ɣ�
�����жϵ�B�Ƿ���ֱ��l�������µ�������˵�����ɣ�
���𰸡���1����A����ֱ��l�������µ�������2����B��ֱ��l�������µ����������������.
��������
��1��ֱ��l��x=1�������A��ֱ��l�ľ���Ϊ2�����������µ����Ķ�������ж�����.
��2���ӵ�C����F���ҳ�ƽ�ƹ��ɣ�������õ�D,E�����꣬���ݵ�E����x���ϣ���������MFD�����Ϊ![]() ���������
���������![]() ��ֵ�����������B�����꣬���������µ����Ķ�������ж�����.
��ֵ�����������B�����꣬���������µ����Ķ�������ж�����.
��1����A����1��a����ֱ��l��x=1��
���A��ֱ��l�ľ���Ϊ2��2��1��
���A����ֱ��l�������µ�����
��2����![]() ��F��1��a+b����
��F��1��a+b����
��������![]() ���������b+1��
���������b+1��
��![]()
�ߵ�E����x���ϣ�
��2a+b+1=0��
��������MFD�����Ϊ![]() ��
��
��![]()
��![]()
��![]() ʱ�����
ʱ�����![]() ����ʱ��
����ʱ��![]() ��ֱ��l�������µ�����
��ֱ��l�������µ�����
��![]() ʱ��
ʱ��![]() ��ʱ
��ʱ![]() ��B��ֱ��l�������µ�����
��B��ֱ��l�������µ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����PΪ��ABC���ߴ�ֱƽ���ߵĽ��㣬��PAC��20������PCB��30����

��1�����PAB�Ķ�����
��2��ֱ��д����APB���ACB��������ϵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC��BEƽ�֡�ABC��AC�ڵ�E������E��EF��BC��AB�ڵ�F��D��BC���ϵ��е㣬����AD��

��1������BAD��55�������C�Ķ�����
��2������FB��FE��������ϵ����֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() �ľ��λ�̳��������С·��
�ľ��λ�̳��������С·��
![]() ��ͼ
��ͼ![]() ��������ܵ�С·�Ŀ�����ȣ���ôС·������Χ�ɵľ���
��������ܵ�С·�Ŀ�����ȣ���ôС·������Χ�ɵľ���![]() �;���
�;���![]() ��������˵�����ɣ�
��������˵�����ɣ�
![]() ��ͼ
��ͼ![]() ���������ŵ�����С·�Ŀ�����ȣ�����С·�Ŀ�
���������ŵ�����С·�Ŀ�����ȣ�����С·�Ŀ�![]() ��
��![]() �ı�ֵΪ����ʱ����ʹС·������Χ�ɵľ���
�ı�ֵΪ����ʱ����ʹС·������Χ�ɵľ���![]() �;���
�;���![]() ���ƣ���˵�����ɣ�
���ƣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��x���ʾһ����������ĵ�·��y���ʾһ���ϱ�����ĵ�·��С����С���ֱ��ʮ��·��O�㴦ͬʱ������С������x����4ǧ��ʱ���ٶ�������ǰ����С������y����5ǧ��/ʱ���ٶ�������ǰ������һ�Ű������λ��ͼ�е�P�㴦��������x�ᡢy��ľ���ֱ���3ǧ��2ǧ�ף�
�ʣ���1���뿪·�ں�����ʱ�䣬��������ù����ľ���ǡ����ȣ�
��2���뿪·�ھ�������ʱ�䣬��������Ź���������λ��ǡ����һ��ֱ���ϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
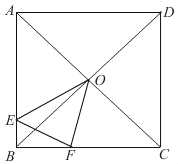
����Ŀ����ͼ��OΪ������ABCD�Խ��ߵĽ��㣬EΪAB����һ�㣬FΪBC����һ�㣬��EBF���ܳ�����BC�ij���
��1����AB=12��BE=3����EF�ij���
��2������EOF�Ķ�����
��3����OE=![]() OF����
OF����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ�
�ϣ�![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ��
Ϊ��![]() �ϵĶ��㣬��ʹ�ı���
�ϵĶ��㣬��ʹ�ı���![]() �ܳ���С�ĵ�
�ܳ���С�ĵ�![]() ������Ϊ�� ��
�������� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ���壬��ִԲ�ӣ���ִ����.��ͼ���������ķ��ӵ�λ���ã���1��0����ʾ�����½Ƿ��ӵ�λ���ã�0����1����ʾ������4öԲ�ӷ������̺����������ӹ���һ����Գ�ͼ�Σ��ŵ�λ���ǣ� ��

A. ����2��1�� B. ����1��1�� C. ����1��0�� D. ����1��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵ���Rt��ABC������BAC=90������E��AC�ϣ��Ҳ����A��C�غ���������ABC���ⲿ������Rt��CED��ʹ��CED=90��������AD���ֱ���AB��ADΪ�ڱ���ƽ���ı���ABFD������AF��
��1����֤����AEF�ǵ���ֱ����������
��2����ͼ2������CED�Ƶ�C��ʱ����ת������E���߶�BC��ʱ������AE����֤��AF=![]() AE��
AE��
��3����ͼ3������CED�Ƶ�C������ʱ����ת����ƽ���ı���ABFDΪ����������CED����ABC���·�ʱ����AB=2![]() ��CE=2�����߶�AE�ij���
��CE=2�����߶�AE�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com