
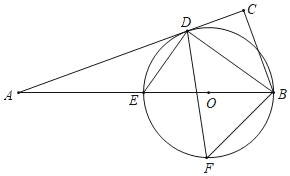
【题目】如图,在△ABC中,∠C=90°,点O为BE上一点,以OB为半径的⊙O交AB于点E,交AC于点D.BD平分∠ABC.
(1)求证:AC为⊙O切线;
(2)点F为![]() 的中点,连接BF,若BC=
的中点,连接BF,若BC=![]() ,BD=8,求⊙O半径及DF的长.
,BD=8,求⊙O半径及DF的长.
【答案】(1)证明见解析(2)7![]()
【解析】
(1)连接OD,根据角平分线的性质得到∠CBD=∠OBD,根据角平分线的定义得到∠ODB=∠OBD,推出OD∥BC,得到∠ADO=∠C=90°,于是得到结论;
(2)由BE为⊙O的直径,得到∠BDE=90°,根据相似三角形的性质得到BE=10,求得⊙O半径OB=5;推出∠EDF=∠BDF=45°,过B作BM⊥DF于M,过E作EN⊥DF于N,连接EF,解直角三角形得到BM=![]() BD=4
BD=4![]() ,EN=
,EN=![]() DE=3
DE=3![]() ,EF=
,EF=![]() BE=5
BE=5![]() ,根据三角形的面积公式列方程即可得到结论.
,根据三角形的面积公式列方程即可得到结论.
(1)证明:连接OD,
∵BD平分∠ABC,
∴∠CBD=∠OBD,
∵OB=OD,
∴∠ODB=∠OBD,
∴∠ODB=∠CBD,
∴OD∥BC,
∴∠ADO=∠C=90°,
∴OD⊥AC,
∴AC为⊙O切线;
(2)解:∵BE为⊙O的直径,
∴∠BDE=90°,
∴∠C=∠BDE,
∵∠CBD=∠EBD,
∴△CBD∽△DBE,
∴![]() ,
,
即![]() ,
,
∴BE=10,
∴⊙O半径OB=5;
∴DE=6,
∵点F为![]() 的中点,
的中点,
∴![]() ,
,
∴∠EDF=∠BDF=45°,
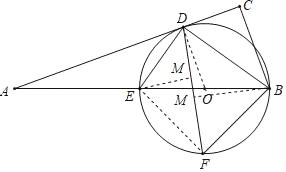
过B作BM⊥DF于M,过E作EN⊥DF于N,连接EF,
∴BM=![]() BD=4
BD=4![]() ,EN=
,EN=![]() DE=3
DE=3![]() ,EF=
,EF=![]() BE=5
BE=5![]() ,
,
∴S四边形BDEF=S△BEF+S△BDE=S△DEF+S△DBF,
∴![]() ×5
×5![]() ×5
×5![]() +
+![]() ×6×8=
×6×8=![]() ×3
×3![]() DF+
DF+![]() ×4
×4![]() DF,
DF,
∴DF=7![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】为创建“国家卫生城市”,进一步优化市中心城区的环境,德州市政府拟对部分路段的人行道地砖、花池、排水管道等公用设施全面更新改造,根据市政建设的需要,须在60天内完成工程.现在甲、乙两个工程队有能力承包这个工程.经调查知道:乙队单独完成此项工程的时间比甲队单独完成多用25天,甲、乙两队合作完成工程需要30天,甲队每天的工程费用2500元,乙队每天的工程费用2000元.
(1)甲、乙两个工程队单独完成各需多少天?
(2)请你设计一种符合要求的施工方案,并求出所需的工程费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
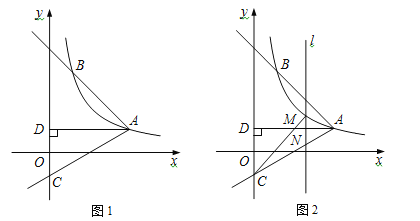
【题目】如图1,反比例函数![]() (x>0)的图象经过点A(
(x>0)的图象经过点A(![]() ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2,M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高【 】
A.40% B.33.4% C.33.3% D.30%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,……,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥1,且n为正整数).
(1)直接写出下列点B1B2,B3的坐标;
(2)写出抛物线L2,L3的解析式,并写出其中一个解析式的求解过程,再猜想抛物线Ln的顶点坐标;
(3)①设A1D1=k1·D1B1,A2D2=k2·D2B2,试判断k1与k2的数量关系并说明理由;
②点D1,D2,…,Dn是否在一条直线上?若是,直接写出这条直线与直线y=x+1的交点坐标;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,□ABCD中,EF过对角线的交点O,如果AB=6cm,AD=5cm,OF=2cm,那么四边形BCEF的周长为( )
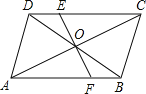
A. 13cmB. 15cmC. 11cmD. 9.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有4个分别写有数字﹣2,﹣1,0,1,2的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字为m,点P的坐标为(m,m2+1),则点P落在抛物线y=﹣4x2+8x+5与x轴所围成的区域内(含边界)的概率是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 所有矩形都是相似的
B. 若线段a=5cm,b=2cm,则a:b=5:2
C. 若线段AB=![]() cm,C是线段AB的黄金分割点,且AC>BC,则AC=
cm,C是线段AB的黄金分割点,且AC>BC,则AC=![]() cm
cm
D. 四条长度依次为lcm,2cm,2cm,4cm的线段是成比例线段
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com