
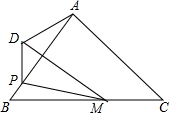
 如图,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,则AD的最小值为$\sqrt{17}$-4.
如图,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,则AD的最小值为$\sqrt{17}$-4. 分析 如图,作辅助圆;根据勾股定理依次求出AE、EM、AM、DM的长度,即可解决问题.
解答 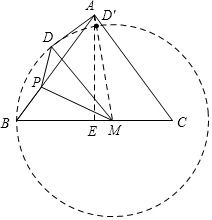 解:如图,由题意得:DM=MB,
解:如图,由题意得:DM=MB,
∴点D在以M为圆心,BM为半径的圆上,作⊙M; 连接AM交⊙M于点D′,此时AD值最小;
过A作AE⊥BC于E,
∵AB=AC=5,
∴BE=EC=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,
由勾股定理得:AE=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵BM=4,
∴EM=4-3=1,
∴AM=$\sqrt{A{E}^{2}+E{M}^{2}}$=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,
∵D′M=BM=4,
∴如图中AD′=AM-D′M=$\sqrt{17}$-4,
即线段AD长的最小值是$\sqrt{17}$-4;
故答案为:$\sqrt{17}$-4.
点评 该题主要考查了翻折变换的性质、勾股定理、最值问题等几何知识点及其应用问题;解题的关键是作辅助圆,从整体上把握题意,准确找出图形中数量关系.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月租费(元/部) | 通讯费(元/分钟) | |
| A种收费标准 | 15 | 0.2 |
| B种收费标准 | 0 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 摸出的是3个白球 | B. | 摸出的是3个黑球 | ||
| C. | 摸出的是2个白球、1个黑球 | D. | 摸出的是2个黑球、1个白球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com