
| AЈ® | 2 | BЈ® | 1 | CЈ® | 4 | DЈ® | 3 |
·ЦОц ёщѕЭ¶юґОёщКЅµДРФЦК¶ФёчРЎМвЅшРРЕР¶ПЈ®
Ѕвґр ЅвЈєЈє$\sqrt{\frac{-9}{-25}}$=$\frac{\sqrt{9}}{\sqrt{25}}$=$\frac{3}{5}$Ј¬ЛщТФўЩХэИ·Ј»
$\sqrt{\frac{b}{a}}$=$\sqrt{\frac{ab}{{a}^{2}}}$=$\frac{\sqrt{ab}}{|a|}$Ј¬ЛщТФўЪґнОуЈ»
$\sqrt{2\frac{1}{4}}$=$\sqrt{\frac{9}{4}}$=$\frac{3}{2}$Ј¬ЛщТФўЫґнОуЈ»
$\sqrt{\frac{4y}{27{x}^{2}}}$=$\sqrt{\frac{12y}{81{x}^{2}}}$=$\frac{2\sqrt{3y}}{9|x|}$Ј¬ЛщТФўЬґнОуЈ®
№КСЎBЈ®
µгЖА ±ѕМвїјІйБЛ¶юґОёщКЅµД»мєПФЛЛгЈєПИ°С¶юґОёщКЅ»ЇОЄЧојт¶юґОёщКЅЈ¬И»єуЅшРР¶юґОёщКЅµДіЛіэФЛЛгЈ¬ФЩєПІўјґїЙЈ®ФЪ¶юґОёщКЅµД»мєПФЛЛгЦРЈ¬ИзДЬЅбєПМвДїМШµгЈ¬Бй»оФЛУГ¶юґОёщКЅµДРФЦКЈ¬СЎФсЗЎµ±µДЅвМвНѕѕ¶Ј¬НщНщДЬК°빦±¶Ј®


 Н¬ІЅБ·П°єУДПґуС§іц°жЙзПµБРґр°ё
Н¬ІЅБ·П°єУДПґуС§іц°жЙзПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
| AЈ® | 2400ЎБЈЁ1-20%Ј© | BЈ® | 2400ЎВЈЁ1-20%Ј© | CЈ® | 2400ЎБЈЁ1+20%Ј© | DЈ® | 2400ЎВЈЁ1+20%Ј© |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
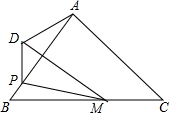 ИзНјЈ¬ФЪЎчABCЦРЈ¬AB=AC=5Ј¬BC=6Ј¬µгMКЗBCЙПТ»µгЈ¬ЗТBM=4Ј¬µгPКЗ±ЯABЙПТ»¶ЇµгЈ¬Б¬ЅУPMЈ¬Ѕ«ЎчBPMСШPM·ХЫµГµЅЎчDPMЈ¬µгDУлµгB¶ФУ¦Ј¬Б¬ЅУADЈ¬ФтADµДЧоРЎЦµОЄ$\sqrt{17}$-4Ј®
ИзНјЈ¬ФЪЎчABCЦРЈ¬AB=AC=5Ј¬BC=6Ј¬µгMКЗBCЙПТ»µгЈ¬ЗТBM=4Ј¬µгPКЗ±ЯABЙПТ»¶ЇµгЈ¬Б¬ЅУPMЈ¬Ѕ«ЎчBPMСШPM·ХЫµГµЅЎчDPMЈ¬µгDУлµгB¶ФУ¦Ј¬Б¬ЅУADЈ¬ФтADµДЧоРЎЦµОЄ$\sqrt{17}$-4Ј®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
 ИзНјЈ¬ТСЦЄABЈ¬AC·Ц±рОЄЎСOµДЦ±ѕ¶єНПТЈ¬DКЗ$\widehat{BC}$µДЦРµгЈ¬DEЎНACУЪEЈ¬DE=3Ј¬AC=8Ј®
ИзНјЈ¬ТСЦЄABЈ¬AC·Ц±рОЄЎСOµДЦ±ѕ¶єНПТЈ¬DКЗ$\widehat{BC}$µДЦРµгЈ¬DEЎНACУЪEЈ¬DE=3Ј¬AC=8Ј®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
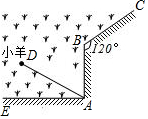 ИзНјЈ¬Т»ёщ3mµДЙюЧУЈ¬Т»¶ЛЛЁФЪЦщЧУAЙПЈ¬БнТ»¶ЛЛЁЧЕТ»Ц»СтЈ¬EABCОЄТ»ЗЅЈ¬AB=2mЈ¬ЎПABC=120ЎгЈ¬ФтСтЧоґуµД»о¶ЇЗшУтµДГж»эКЗЈЁЎЎЎЎЈ©
ИзНјЈ¬Т»ёщ3mµДЙюЧУЈ¬Т»¶ЛЛЁФЪЦщЧУAЙПЈ¬БнТ»¶ЛЛЁЧЕТ»Ц»СтЈ¬EABCОЄТ»ЗЅЈ¬AB=2mЈ¬ЎПABC=120ЎгЈ¬ФтСтЧоґуµД»о¶ЇЗшУтµДГж»эКЗЈЁЎЎЎЎЈ©| AЈ® | $\frac{9}{4}$¦Р | BЈ® | 3¦Р | CЈ® | $\frac{29}{12}$¦Р | DЈ® | $\frac{1}{3}$¦Р |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com