
 ��һ���㹻���������ֽƬ������ͼ��ʾ�������ĸ���С��״һ���������Σ�Ȼ����һ���������ٰ�ͬ���ķ��������ĸ�С�����Σ����ѭ����ȥ����ͳ��ÿ�μ��������εĸ�����
��һ���㹻���������ֽƬ������ͼ��ʾ�������ĸ���С��״һ���������Σ�Ȼ����һ���������ٰ�ͬ���ķ��������ĸ�С�����Σ����ѭ����ȥ����ͳ��ÿ�μ��������εĸ�����| ���Ĵ�����n���� | 1 | 2 | 3 | 4 | �� | n |
| ���������n�� | �� |
���� ��1���ֱ����ó��𰸷��֣�ÿ��һ�Σ�������4�������εĻ���������3�������n�ι���4+3��n-1��=3n+1�������Σ�
��2�����ã�1���еļ��㷽������������ô𰸼��ɣ�
��3��ÿ�����α߳�����ԭ����һ�룬�ɴ˽�һ���ó��𰸼��ɣ�
��� �⣺��1��������£�
| �Ĵ�����n���� | 1 | 2 | 3 | 4 | �� | n |
| ���������n�� | 4 | 7 | 10 | 13 | �� | S=3n+1 |
���� ���⿼��ͼ�εı仯���ɣ��ҳ�ͼ��֮�����ϵ���ó����ֵ�������ɣ����ù��ɽ�����⣮


 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
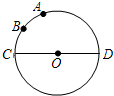 ��֪��O��ֱ��CDΪ4��$\widehat{AC}$�Ķ���Ϊ80�㣬��B��$\widehat{AC}$���е㣬��P��ֱ��CD���ƶ�����BP+AP����СֵΪ2$\sqrt{3}$��
��֪��O��ֱ��CDΪ4��$\widehat{AC}$�Ķ���Ϊ80�㣬��B��$\widehat{AC}$���е㣬��P��ֱ��CD���ƶ�����BP+AP����СֵΪ2$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com