Question

6．在6米高的路灯下，身高1.5米的哥哥的影长为1米，身高1.2米的弟弟的影长为2米，那么哥哥和弟弟之间的距离x的取值是5米或11米．

Answer 1

分析 根据题意画出图形，分哥哥和弟弟在路灯的同一侧与两侧进行讨论．

解答 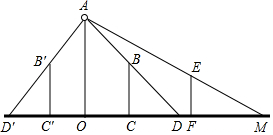解：如图，当哥哥在BC位置时，
∵OA=6米，BC=1.5米，CD-1米，EF=1.2米，FM=2米，
∵BC⊥OM，
∴△BCD∽△AOD，
∴$\frac{CD}{CD+OC}$=$\frac{BC}{OA}$，即$\frac{1}{1+OC}$=$\frac{1.5}{6}$，解得OC=3米．
同理，∵△MEF∽△MAO，
∴$\frac{MF}{MF+CF+OC}$=$\frac{EF}{OA}$，即$\frac{2}{2+CF+3}$=$\frac{1.2}{6}$，解得CF=5（米），
∴此时，哥哥和弟弟之间的距离x的取值是5米；
当哥哥在B′C′的位置时，同理可得，OC′=3米，
∴C′F=3+3+5=11（米），
∴此时，哥哥和弟弟之间的距离x的取值是11米．
故答案为：5米或11米．

点评 本题考查的是相似三角形的应用，在解答此题时要注意分两种情况进行讨论．