练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：关于的一元二次方程，

    （1）求证：方程有两个不相等的实数根且其中一个根为定值。

    （2）设方程的两个实数根分别为， (其中<)。若y是关于m的函数，且，求这个函数的解析式；并求当自变量的取值范围满足什么条件时， 。

    【答案】（1）证明见解析；

    （2）这个函数的解析式为y=5-2m，当m≥1时，

    【解析】试题分析：（1）求出一元二次方程的根的判别式，然后整理成完全平方的形式，然后判断其取值范围，即可证明；

    （2）按要求代入即可.

    试题解析：（1）△=（3m+2）-4 m(2m+2)=9m +12m+4-8 m -8m= m +4m+4=(m+2)

    ∵ m＞0，

    ∴(m+2) ＞0

    即△＞0

    ∴方程有两个不相等的实数根

    ∵x=

    ∴

    ∴方程有一个根为定值1.

    （2）=7-2m-2=5-2m

    当 即5-2m≤3 m

    ∴m≥1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】平行四边形ABCD中，E，F是对角线BD上的两点， 如果添加一个条件使△ABE≌△CDF，则添加的条件不能是（　　）

    A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：

    （1）（x﹣3）（x﹣1）=3；

    （2）（x+1）2=6（x+1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

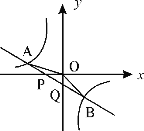
    【题目】如图，已知直线 与x轴、y轴相交于P、Q两点，与y=的图像相交于A（－2，m）、B（1，n）两点，连接OA、OB．给出下列结论： ①k1k2＜0；②m+n=0； ③S△AOP= S△BOQ；④不等式k1x+b＞的解集是x＜－2或0＜x＜1，其中正确的结论的序号是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若使等式(－4)□(－6)＝2成立，则□中应填入的运算符号是(　　)

    A. ＋ B. － C. × D. ÷

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】汽车在匀速行驶过程中，路程s、速度v、时间t之间的关系为s＝vt，下列说法正确的是（　　）

    A. s、v、t都是变量B. s、t是变量，v是常量

    C. v、t是变量，s是常量D. s、v是变量，t是常量

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算结果正确的是（　　）

    A. a4﹒a2=a8 B. (a5)2=a7 C. (a-b)2=a2-b2 D. (ab)2=a2b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“激情同在”第23届冬奥会于2018年2月在韩国平昌郡举行，场馆的建筑面积约是358 000平方米，将358 000用科学记数法表示为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

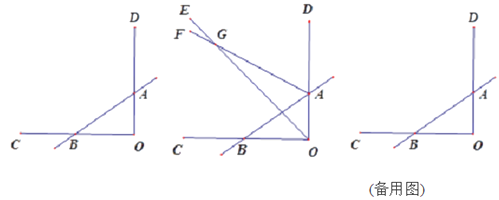
    【题目】已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE与射线AF交于点G.

    （1）若OE平分∠BOA，AF平分∠BAD，∠OBA=42°，则∠OGA= ；

    （2）若∠GOA=∠BOA，∠GAD=∠BAD，∠OBA=42°，则∠OGA= ；

    （3）将（2）中的“∠OBA=42°”改为“∠OBA=”，其它条件不变，求∠OGA的度数.（用含的代数式表示）

    （4）若OE将∠BOA分成1︰2两部分，AF平分∠BAD，∠ABO=（30°<<90°） ，求∠OGA的度数.（用含的代数式表示）

    查看答案和解析>>

    同步练习册答案