
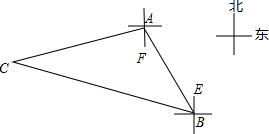
分析 过点A作AD⊥BC交BC于一点D,根据题意得∠FAE=30°,∠CBE=75°,利用三角形的外角的性质得到∠C=180°-75°-30°-45°=30°,然后在Rt△ADB中,求得AD=100米,CD=$100\sqrt{3}$米后即可求得三角形ABC的周长.
解答 解:过点A作AD⊥BC交BC于一点D,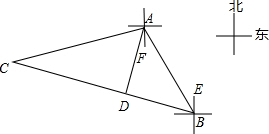
根据题意得∠FAE=30°,∠CBE=75°,
故∠ABE=∠FAE=30°,
∴∠ABC=45°,
∴∠DAB=∠ABC=45°,
∴∠C=180°-75°-30°-45°=30°,
在Rt△ADC中,
∵AC=200米,∠C=30°,
∴AD=100米,CD=$100\sqrt{3}$米
在Rt△ADB中,
∵AD=00米,∠ABC=45°,
∴AB=100$\sqrt{2}$米,DB=100米
∴BC=CD+DB=(100+100$\sqrt{3}$)米,
∴三角形ABC的周长为200+100$\sqrt{3}$+100+100$\sqrt{2}$≈615米
沿三角形绿化区的周边小路跑两圈共跑了约1230米.
点评 本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形模型并求解.


科目:初中数学 来源: 题型:选择题
| A. | 甲地:总体平均数为3,中位数为4 | |
| B. | 乙地:中位数为2,众数为3 | |
| C. | 丙地:总体平均数为2,总体方差为3 | |
| D. | 丁地:总体平均数为1,总体方差大于0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
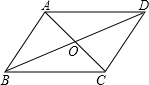 如图,?ABCD的对角线AC、BD交于点O.
如图,?ABCD的对角线AC、BD交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com