
【题目】如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处。
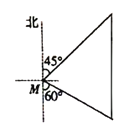
(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示):
(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间(结果精确到0.1小时)。(参考数据:![]() )
)
【答案】(1)、90![]() 海里;(2)、7.4小时.
海里;(2)、7.4小时.
【解析】
试题分析:(1)、过点M作MD⊥AB于点D,根据AM=180海里以及△AMD的三角函数求出MD的长度;(2)、根据三角函数求出MB的长度,然后计算.
试题解析:(1)、过点M作MD⊥AB于点D, ∵∠AME=45°, ∴∠AMD=∠MAD=45°, ∵AM=180海里, ∴MD=AMcos45°=90![]() (海里), 答:渔船从A到B的航行过程中与小岛M之间的最小距离是90
(海里), 答:渔船从A到B的航行过程中与小岛M之间的最小距离是90![]() 海里;
海里;
(2)、在Rt△DMB中, ∵∠BMF=60°,∴∠DMB=30°, ∵MD=90![]() 海里, ∴MB=60
海里, ∴MB=60![]() 海里,
海里,
∴60![]() ÷20≈7.4(小时),
÷20≈7.4(小时),
答:渔船从B到达小岛M的航行时间约为7.4小时.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
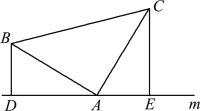
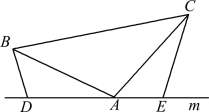
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C; ②∠AEF=∠AFE; ③∠EBC=∠C;④AG⊥EF.正确结论有( )
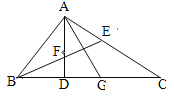
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位同学做一道题,已知两个多项式A,B,计算A+B,他误将A+B看作A-B,求得9x2-2x+7,若B=x2+3x-2,你能否帮助他求得正确答案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com